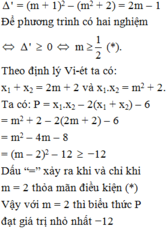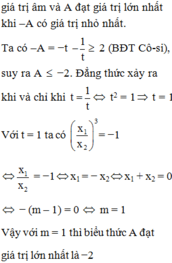Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Với m= 2, ta có 2 x 2 − 4 x + 2 = 0 ⇔ x = 1
b) Phương trình (1) có hai nghiệm x 1 , x 2 khi và chỉ khi Δ ' ≥ 0 ⇔ − 2 ≤ m ≤ 2
Theo Vi-et , ta có: x 1 + x 2 = m 1 x 1 . x 2 = m 2 − 2 2 2
Theo đề bài ta có: A = 2 x 1 x 2 − x 1 − x 2 − 4 = m 2 − 2 − m − 4 = m − 3 m + 2
Do − 2 ≤ m ≤ 2 nên m + 2 ≥ 0 , m − 3 ≤ 0 . Suy ra A = m + 2 − m + 3 = − m 2 + m + 6 = − m − 1 2 2 + 25 4 ≤ 25 4
Vậy MaxA = 25 4 khi m = 1 2 .

a. + Với m = − 1 2 phương trình (1) trở thành x 2 − 4 x = 0 ⇔ x = 0 x = 4 .
+ Vậy khi m = − 1 2 phương trình có hai nghiệm x= 0 và x= 4.
b. + Phương trình có hai nghiệm dương phân biệt khi
Δ = 2 m + 5 2 − 4 2 m + 1 > 0 x 1 + x 2 = 2 m + 5 > 0 x 1 . x 2 = 2 m + 1 > 0
+ Ta có Δ = 2 m + 5 2 − 4 2 m + 1 = 4 m 2 + 12 m + 21 = 2 m + 3 2 + 12 > 0 , ∀ m ∈ R
+ Giải được điều kiện m > − 1 2 (*).
+ Do P>0 nên P đạt nhỏ nhất khi P 2 nhỏ nhất.
+ Ta có P 2 = x 1 + x 2 − 2 x 1 x 2 = 2 m + 5 − 2 2 m + 1 = 2 m + 1 − 1 2 + 3 ≥ 3 ( ∀ m > − 1 2 ) ⇒ P ≥ 3 ( ∀ m > − 1 2 ) .
và P = 3 khi m= 0 (thoả mãn (*)).
+ Vậy giá trị nhỏ nhất P = 3 khi m= 0.

Δ=(2m-2)^2-4(2m-5)
=4m^2-8m+4-8m+20
=4m^2-16m+24
=4m^2-16m+16+8=(2m-4)^2+8>=8>0 với mọi m
=>Phương trình luôn có hai nghiệm phân biệt
\(B=\dfrac{x_1^2}{x^2_2}+\dfrac{x_2^2}{x_1^2}\)
\(=\dfrac{x_1^4+x_2^4}{\left(x_1\cdot x_2\right)^2}=\dfrac{\left(x_1^2+x_2^2\right)^2-2\left(x_1\cdot x_2\right)^2}{\left(x_1\cdot x_2\right)^2}\)
\(=\dfrac{\left[\left(2m-2\right)^2-2\left(2m-5\right)\right]^2-2\left(2m-5\right)^2}{\left(2m-5\right)^2}\)
\(=\dfrac{\left(4m^2-8m+4-4m+10\right)^2}{\left(2m-5\right)^2}-2\)
\(=\left(\dfrac{4m^2-12m+14}{2m-5}\right)^2-2\)
\(=\left(\dfrac{4m^2-10m-2m+5+9}{2m-5}\right)^2-2\)
\(=\left(2m-1+\dfrac{9}{2m-5}\right)^2-2\)
Để B nguyên thì \(2m-5\in\left\{1;-1;3;-3;9;-9\right\}\)
=>\(m\in\left\{3;2;4;1;7\right\}\)

a) Thay m=0 vào phương trình (1), ta được:
\(x^2-2\cdot\left(0-1\right)x+0^2-3m=0\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow x\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy: Khi m=0 thì S={0;-2}

a) Phương trình có hai nghiệm phân biệt khi:
\(\Delta=9-4\left(m+1\right)>0\) \(\Leftrightarrow m< \dfrac{5}{4}\)
Vậy \(\ m< \dfrac{5}{4}\) thì pt có hai nghiệm phân biệt.
b) Áp dụng hệ thức viet có:
\(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1.x_2=m+1\end{matrix}\right.\)
\(P=\left(x_1+x_2\right)^2-4x_1.x_2+7m+5.x_1x_2\)
\(=9-4\left(m+1\right)+7m+5\left(m+1\right)\)
\(=8m+10\)
Không tồn tại giá trị lớn nhất. Em xem lại đề
Trên đó em ko hề có ghi là tìm m để pt có 2 nghiệm phân biệt. Vậy nên phải là m \(\le\dfrac{5}{4}\). KQ: Giá trị lớn nhất của P = 20 khi m = \(\dfrac{5}{4}\)

a) Xét pt đã cho có \(a=m^2+m+1\); \(b=-\left(m^2+2m+2\right)\); \(c=-1\)
Nhận thấy rằng \(ac=\left(m^2+m+1\right)\left(-1\right)=-\left(m^2+m+1\right)\)
\(=-\left(m^2+2m.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\right)=-\left(m+\dfrac{1}{2}\right)^2-\dfrac{3}{4}\)
Vì \(-\left(m+\dfrac{1}{2}\right)^2\le0\) và \(-\dfrac{3}{4}< 0\) nên \(-\left(m+\dfrac{1}{2}\right)^2-\dfrac{3}{4}< 0\) hay \(ac< 0\). Vậy pt đã cho luôn có 2 nghiệm trái dấu.
b) Theo câu a, ta đã chứng minh được pt đã cho luôn có 2 nghiệm trái dấu \(x_1,x_2\).
Áp dụng hệ thức Vi-ét, ta có \(S=x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m^2+2m+2\right)}{m^2+m+1}=\dfrac{m^2+2m+2}{m^2+m+1}\)
Nhận thấy \(m^2+m+1\ne0\) nên ta có:
\(\left(m^2+m+1\right)S=m^2+2m+2\) \(\Leftrightarrow Sm^2+Sm+S-m^2-2m-2=0\)\(\Leftrightarrow\left(S-1\right)m^2+\left(S-2\right)m+\left(S-2\right)=0\)(*)
pt (*) có \(\Delta=\left(S-2\right)^2-4\left(S-1\right)\left(S-2\right)\)\(=S^2-4S+4-4\left(S^2-3S+2\right)\)\(=S^2-4S+4-4S^2+12S-8\)\(=-3S^2+8S-4\)
Để pt (*) có nghiệm thì \(\Delta\ge0\) hay \(-3S^2+8S-4\ge0\)\(\Leftrightarrow-3S^2+6S+2S-4\ge0\)\(\Leftrightarrow-3S\left(S-2\right)+2\left(S-2\right)\ge0\) \(\Leftrightarrow\left(S-2\right)\left(2-3S\right)\ge0\)
Ta xét 2 trường hợp:
TH1: \(\left\{{}\begin{matrix}S-2\ge0\\2-3S\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S\ge2\\S\le\dfrac{2}{3}\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}S-2\le0\\2-3S\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S\le2\\S\ge\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\dfrac{2}{3}\le S\le2\) (nhận)
Khi \(S=\dfrac{2}{3}\) thì (*) \(\Leftrightarrow\left(\dfrac{2}{3}-1\right)m^2+\left(\dfrac{2}{3}-2\right)m+\dfrac{2}{3}-2=0\)\(\Leftrightarrow-\dfrac{1}{3}m^2-\dfrac{4}{3}m-\dfrac{4}{3}=0\)\(\Leftrightarrow m^2+4m+4=0\)
\(\Leftrightarrow\left(m+2\right)^2=0\) \(\Leftrightarrow m+2=0\) \(\Leftrightarrow m=-2\)
Khi \(S=2\) thì (*) \(\Leftrightarrow\left(2-1\right)m^2+\left(2-2\right)m+2-2=0\)\(\Leftrightarrow m^2=0\)
\(\Leftrightarrow m=0\)
Vậy GTNN của S là \(\dfrac{2}{3}\) khi \(m=-2\) và GTLN của S là \(2\) khi \(m=0\)

\(x^2+2\left(2m-1\right)x+3\left(m^2-1\right)=0\)
\(a,\) Để pt có nghiệm thì \(\Delta\ge0\)
\(\Rightarrow\left[2\left(2m-1\right)\right]^2-4\left[3\left(m^2-1\right)\right]\ge0\)
\(\Rightarrow4\left(4m^2-4m+1\right)-4\left(3m^2-3\right)\ge0\)
\(\Rightarrow16m^2-16m+4-12m^2+12\ge0\)
\(\Rightarrow4m^2-16m+16\ge0\)
\(\Rightarrow\left(2m-4\right)^2\ge0\)
Vậy pt có nghiệm với mọi m.
b, Theo viét : \(\left\{{}\begin{matrix}x_1+x_2=-2\left(2m-1\right)\\x_1x_2=3\left(m^2-1\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=-4m+2\\x_1x_2=3m^2-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{-2+x_1+x_2}{4}\\x_1x_2=3\left(\dfrac{-2+x_1+x_2}{4}\right)^2-3\end{matrix}\right.\)
Vậy......