Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Pt đã cho có 2 nghiệm trái dấu khi:
\(ac< 0\Leftrightarrow\left(m+1\right)\left(m-2\right)< 0\)
\(\Leftrightarrow-1< m< 2\)

Với m = 1 phương trình đã cho có dạng
2 x 2 + 2 = 0 .
Phương trình này vô nghiệm, nên phương án A bị loại. Với m = -1 phương trình đã cho trở thành phương trình bậc nhất 6x + 2 = 0 chỉ có một nghiệm nên phương án B bị loại.
Với m = 2 phương trình đã cho trở thành phương trình
3 x 2 – 3 x + 2 = 0 .
Phương trình này vô nghiệm, nên phương án D bị loại.
Đáp án: C

a, ĐK: \(x\le-1,x\ge3\)
\(pt\Leftrightarrow2\left(x^2-2x-3\right)+\sqrt{x^2-2x-3}-3=0\)
\(\Leftrightarrow\left(2\sqrt{x^2-2x-3}+3\right).\left(\sqrt{x^2-2x-3}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2-2x-3}=-\dfrac{3}{2}\left(l\right)\\\sqrt{x^2-2x-3}=1\end{matrix}\right.\)
\(\Leftrightarrow x^2-2x-3=1\)
\(\Leftrightarrow x^2-2x-4=0\)
\(\Leftrightarrow x=1\pm\sqrt{5}\left(tm\right)\)
b, ĐK: \(-2\le x\le2\)
Đặt \(\sqrt{2+x}-2\sqrt{2-x}=t\Rightarrow t^2=10-3x-4\sqrt{4-x^2}\)
Khi đó phương trình tương đương:
\(3t-t^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=0\\t=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2+x}-2\sqrt{2-x}=0\\\sqrt{2+x}-2\sqrt{2-x}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2+x=8-4x\\2+x=17-4x+12\sqrt{2-x}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{5}\left(tm\right)\\5x-15=12\sqrt{2-x}\left(1\right)\end{matrix}\right.\)
Vì \(-2\le x\le2\Rightarrow5x-15< 0\Rightarrow\left(1\right)\) vô nghiệm
Vậy phương trình đã cho có nghiệm \(x=\dfrac{6}{5}\)

\(\Leftrightarrow\left\{{}\begin{matrix}m^2-1=0\\m^2-2m-3\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\pm1\\m\ne-1;m\ne3\end{matrix}\right.\Leftrightarrow m=1\)
Chọn A

1.
Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)
Pt trở thành:
\(4t=t^2-5+2m-1\)
\(\Leftrightarrow t^2-4t+2m-6=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)
2.
Để pt đã cho có 2 nghiệm:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)
Khi đó:
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)
\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)

Ta có:
m ( x - m + 2 ) = m ( x - 1 ) + 2 ⇔ m x - m 2 + 2 m = m x - m + 2 ⇔ 0 x = m 2 - 3 m + 2 ( * )
Nếu m= 1 hoặc m= 2 thì phương trình (*) trở thành: 0x = 0 luôn đúng với mọi x nên phương trình có vô số nghiệm.
Nếu m ≠ 1 ; m ≠ 2 thì vế phải ≠ 0 nên phương trình đã cho vô nghiệm.
Chọn đáp án là D.

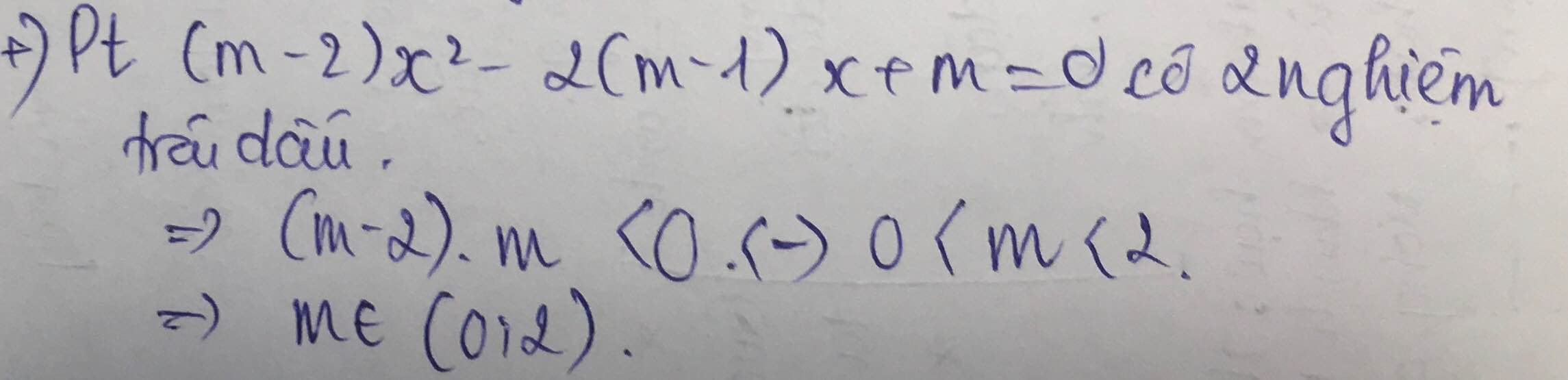

Trước hết phải xét điều kiện để phương trình x 2 - 2 m - 1 x + m 2 - 3 m + 4 = 0 có nghiệm: ∆ ' = m - 1 2 - m 2 - 3 m + 4 = m - 3 > 0 hay m > 3.
Từ đó thấy ngay các phương án A, B, C đều sai.
Khi m = 4 thì phương trình đã cho có 2 nghiệm .
Áp dụng hệ thức Vi- et ta có:
x 1 + x 2 = 2 m - 1 = 2 . 4 - 1 = 6 x 1 . x 2 = m 2 - 3 m + 4 = 4 2 - 3 . 4 + 4 = 8
Khi đó; x 1 2 + x 2 2 = x 1 + x 2 2 - 2 x 1 . x 2 = 6 2 - 2 . 8 = 20