Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách này của mình là suy đoán thui nha
Từ HPT trên: \(\frac{x}{a-q}+\frac{y}{b-q}+\frac{z}{c-q}=\frac{x}{a-p}+\frac{y}{b-p}+\frac{z}{c-p}\)
\(\Leftrightarrow\left(p-q\right)\left[\frac{x}{\left(a-p\right)\left(a-q\right)}+\frac{y}{\left(b-p\right)\left(b-q\right)}+\frac{z}{\left(c-q\right)\left(c-p\right)}\right]=0\)
Chia TH:
TH1:p=q
Tương tự p=r thì cũng thu về p=q=r
TH2: nguyên cái trong ngoặc vuông
Tương đương với: \(ax+by+cz=r\left(x+y+z\right)\)
Tương tự: \(\hept{\begin{cases}ax+by+cz=p\left(x+y+z\right)\\ax+by+cz=q\left(x+y+z\right)\end{cases}}\)
Cũng thu đc p=q=r
Do đó từ 2 TH cũng thu về PT:
\(\frac{x}{a-q}+\frac{y}{b-q}+\frac{z}{c-q}=1\)
Rồi vậy không biết làm tiếp :D
À, xin lỗi, mình đánh bị thiếu điều kiện, mình sửa lại rồi đó

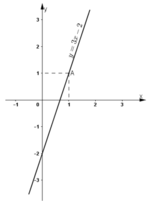
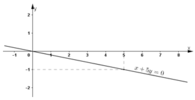
a) 3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x = 2/3 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (2/3 ; 0).
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (2/3 ; 0) và (0; -2).
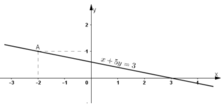
b) x + 5y = 3 (2)
⇔ x = 3 – 5y
Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.
+ Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).
+ Tại x = 0 thì y=3/5 ⇒ Đường thẳng đi qua điểm (0; 3/5).
Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0; 3/5).
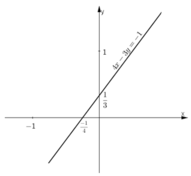
c) 4x – 3y = -1
⇔ 3y = 4x + 1
⇔ 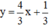
Vậy phương trình có nghiệm tổng quát là (x;4/3x+1/3)(x ∈ R).
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 1/3
Đường thẳng đi qua điểm (0;1/3) .
+ Tại y = 0 thì x = -1/4
Đường thẳng đi qua điểm (-1/4;0) .
Vậy đường thẳng 4x – 3y = -1 đi qua (0;1/3) và (-1/4;0).
d) x + 5y = 0
⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
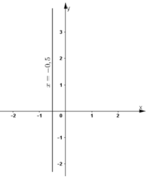
e) 4x + 0y = -2
⇔ 4x = -2 ⇔ 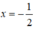
Phương trình có nghiệm tổng quát (-0,5; y)(y ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng x = -0,5 đi qua điểm (-0,5; 0) và song song với trục tung.
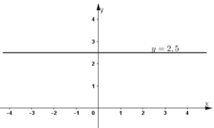
f) 0x + 2y = 5
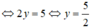
Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.

Giả sử rằng \(\left(x,y\right)\) là nghiệm nguyên của phương trình \(ax+by=c.\) Suy ra \(a\left(x+y\right)+y\left(b-a\right)=c.\) Vì \(b-a\vdots c\to a\left(x+y\right)\vdots c\). Mà \(a,c\) là hai số nguyên tố cùng nhau nên \(x+y\vdots c.\)


Ta có với a ≠ 0; b ≠ 0 thì ax + by = c ⇔ by = −ax + c ⇔ y = − a b x + c b
Nghiệm của phương trình được biểu diễn bởi x ∈ R y = − a b x + c b
Đáp án: A