DA
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DA
2
10 tháng 5 2021
`-4x-6=|2x+4|(x<=-2/3)`
`<=>` $\left[ \begin{array}{l}2x+4=4x+6\\2x+4=-6-3x\end{array} \right.$
`<=>` $\left[ \begin{array}{l}2x=-2\\5x=-10\end{array} \right.$
`<=>` $\left[ \begin{array}{l}x=-1\\x=-2(tm)\end{array} \right.$
Vậy `S={-1,-2}`
DA
2
10 tháng 5 2021
`|2x+4|=-4x+6(x<=3/2)`
`<=>` $\left[ \begin{array}{l}2x+4=4x-6\\2x+2=6-4x\end{array} \right.$
`<=>` $\left[ \begin{array}{l}2x=10\\6x=4\end{array} \right.$
`<=>` $\left[ \begin{array}{l}x=5\\x=\dfrac23\end{array} \right.$
Vậy `S={2/3,5}`
CM
27 tháng 3 2018
+) Thay x = 5 vào phương trình 2 x − 3 = x + 2 x − 4 ta được
2.5 − 3 = 5 + 2 5 − 4 ⇔ 7 = 7 1 = 7
Vậy 5 là nghiệm của phương trình 2 x − 3 = x + 2 x − 4 khẳng định (I) đúng.
+) Tập nghiệm của phương trình 7 – x = 2x – 8 là x = 5 là khẳng định sai vì kết luận x = 5 không phải là tập nghiệm.
+) Ta có: 10 - 2x = 0 ⇔ 2x = 10 ⇔ x = 5
Vậy tập nghiệm của phương trình là S = {5}.
Do đó khẳng định (III) là đúng.
Vậy có hai mệnh đề đúng.
Đáp án cần chọn là: C
CM
11 tháng 4 2017
a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình 
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 
14 tháng 3 2022
a: Thay x=-2 vào pt,ta được:
-8+4a+8-4=0
=>4a-4=0
hay a=1
b: Pt sẽ là \(x^3+x^2-4x-4=0\)
\(\Leftrightarrow x^2\left(x+1\right)-4\left(x+1\right)=0\)
=>(x+1)(x-2)(x+2)=0
hay \(x\in\left\{-1;2;-2\right\}\)
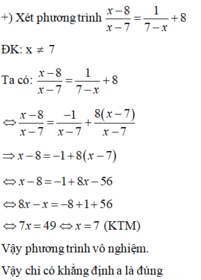
`-4x-3=|2x+4|(x<=-3/4)`
`<=>` $\left[ \begin{array}{l}2x+4=4x+3\\2x+4=-3-4x\end{array} \right.$
`<=>` $\left[ \begin{array}{l}2x=1\\6x=-7\end{array} \right.$
`<=>` $\left[ \begin{array}{l}x=\dfrac12(l)\\x=-\dfrac76(tm)\end{array} \right.$
Vậy `S={-7/6}`
\(\left|2x+4\right|=2x+4\) khi \(2x+4\ge0\Leftrightarrow x\ge-2\)
Ta được phương trình :
\(-4x-3=2x+4\)
\(\Leftrightarrow-4x-2x=4+3\)
\(\Leftrightarrow-6x=7\Leftrightarrow x=-\dfrac{7}{6}\)(TMĐK)
\(\left|2x+4\right|=-\left(2x+4\right)\) khi \(2x+4< 0\Leftrightarrow x< -2\)
Ta được phương trình :
\(-4x-3=-\left(2x+4\right)\)
\(\Leftrightarrow-4x-3=-2x-4\)
\(\Leftrightarrow-4x+2x=-4+3\)
\(\Leftrightarrow-2x=-1\Leftrightarrow x=\dfrac{1}{2}\)(KTMĐK)
Vậy \(S=\left\{-\dfrac{7}{6}\right\}\)