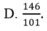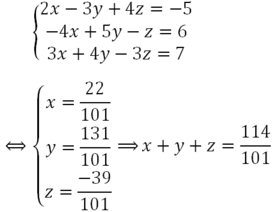Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đây không phải là dạng của phương trình đường tròn (hệ số \({y^2}\) bằng -1).
b) Vì \({a^2} + {b^2} - c = {1^2} + {\left( { - 2} \right)^2} - 6 < 0\) nên phương trình đã cho không là phương trình tròn.
c) Vì \({a^2} + {b^2} - c = {\left( { - 3} \right)^2} + {2^2} - 1 = 11 > 0\) nên phương trình đã cho là phương trình tròn có tâm \(I\left( { - 3;2} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} = \sqrt {11} \).

Tham khảo:
a) Vì \(0 - 2.0 + 6 = 6 > 0\) nên (0;0) là một nghiệm của bất phương trình đã cho.
b) Vì \(0 - 2.1 + 6 = 4 > 0\) nên (0;1) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.0 + 6 = 7 > 0\) nên (1;0) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.1 + 6 = 5 > 0\) nên (1;1) là một nghiệm của bất phương trình đã cho.
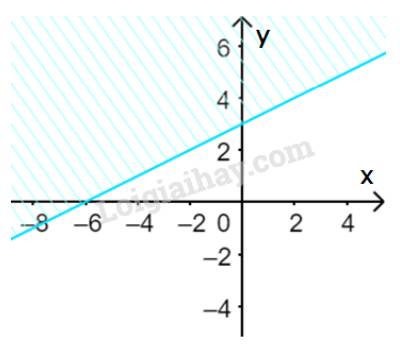
c) Vẽ đường thẳng \(\Delta :x - 2y + 6 = 0\) đi qua hai điểm \(A(0;3)\) và \(B\left( { - 2;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 2.0 + 6 = 6 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)

a) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = 1,b = 2,c = - 20\)
Ta có \({a^2} + {b^2} - c = 1 + 4 + 20 = 25 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I(1;2)\) và có bán kính \(R = \sqrt {25} = 5\)
b) Phương trình \({\left( {x + 5} \right)^2} + {\left( {y + 1} \right)^2} = 121\) là phương trình dường tròn với tâm \(I( - 5; - 1)\) và bán kinh \(R = \sqrt {121} = 11\)
c) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = - 3,b = - 2,c = - 2\)
Ta có \({a^2} + {b^2} - c = 9 + 4 + 2 = 15 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I( - 3; - 2)\) và có bán kính \(R = \sqrt {15} \)
d) Phương trình không có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) nên phương trình đã cho không là phương trình đường tròn