
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

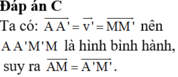

Trong mặt phẳng với hệ trục Oxy, ảnh của điểm M(x;y) qua phép tịnh tiến vectơ là:
A. M' (a - x; b - y)
B. M' (x + b; y + a)
C. M' (-x + a; y + b)
D. M' (x + a; y + b)
Giải thích;
\(M'\left(x';y'\right)=T_{\overrightarrow{v}}\left(M\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x'-x=a\\y'-y=b\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x'=x+a\\y'=y+b\end{matrix}\right.\)
\(\Rightarrow M'\left(x+a;y+b\right)\)
Chọn D.

Đáp án A đúng, \(\overrightarrow{AM}=\overrightarrow{A'M'}\)

Đáp án D
Phát biểuđúng: a , c, e, f, g, i, j, l
b. Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó có thể là phép tịnh tiến
d. Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính
h. Với bất kì 2 điểm A, B và ảnh A’, B’ của chúng qua 1 phép dời hình, ta luôn có AB = A’B’.
k. Nếu phép dời hình biến điểm A thành điểm B thì nó cũng biến điểm B thành A (phát biểu không đúng với phép tịnh tiến)