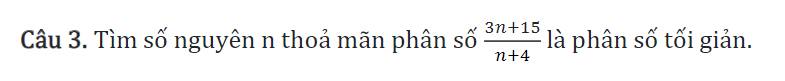Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(d=\left(3n+2,2n+7\right)\).
Suy ra \(\hept{\begin{cases}3n+2⋮d\\2n+7⋮d\end{cases}}\Rightarrow3\left(2n+7\right)-2\left(3n+2\right)=17⋮d\).
\(\Rightarrow\orbr{\begin{cases}d=1\\d=17\end{cases}}\)
Để \(\frac{3n+2}{2n+7}\)là phân số tối giản thì \(d\ne17\)do đó \(3n+2\ne17k\Leftrightarrow n\ne\frac{17k-2}{3}\left(k\inℤ\right)\).

Gọi \(d=ƯC\left(3n+15,n+4\right)\)
\(\Rightarrow\left\{{}\begin{matrix}3n+15⋮d\\n+4⋮d\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}3n+15⋮d\\3n+12⋮d\end{matrix}\right.\)
\(\Rightarrow3⋮d\)
\(\Rightarrow d\inƯ\left(3\right)=\left\{1,3\right\}\)
Thay vào
\(\Rightarrow d=1\)
Để 3n+15/n+4 là PSTG thì 3n+15 chia hết cho n+4
Mà n+4 cũng chia hết cho n+4 => 3(n+4) chia hết cho n+4 =>3n+12 chia hết cho n+4
=>(3n+12)-(3n+4) chia hết cho n+4
=>3n+12-3n-4 chia hết cho n+4
=>8 chia hết cho n+4
=>n+4 thuộc Ư(8)={1; -1 ;2; -2 ;4; -4 ;8; -8 } , ta có bản
| n+4 | 1 | -1 | 2 | -2 | 4 | -4 | 8 | -8 |
| n | -3 | -5 | -2 | -6 | 0 | -8 | 4 | -12 |
Vậy n = {-3; -5; -2; -6; 0; -8; 4; -12}