Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bác học lớp 9 phải ko bài này khá đơn giản mình thấy ai cũng làm đc chỉ cần độg não thui chứ bác hỏi thế rùi vô phòng thi thì sao lớp 9 phải tự học thui

a)
\(\left(P\right):y=x^2\)
Ta có bảng
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 1 | 0 | 1 | 4 |
Vậy đồ thị hàm số \(y=x^2\) là một parabol lần lượt đi qua các điểm
\(\left(-2;4\right),\left(-1;1\right),\left(0;0\right),\left(1;1\right),\left(2;4\right)\)
Bạn tự vẽ nhé
\(\left(d\right):y=-2x+3\)
Cho \(y=0\Rightarrow x=\dfrac{3}{2}\Rightarrow A\left(\dfrac{3}{2};0\right)\in Ox\)
Cho \(x=0\Rightarrow y=3\Rightarrow B\left(0;3\right)\in Oy\)
Vẽ đường thẳng AB ta được đths \(y=-2x+3\)
Bạn tự bổ sung vào hình vẽ nhé
b) Xét PTHĐGĐ của \(\left(P\right),\left(d\right)\) là nghiệm của phương trình
\(x^2=-2x+3\\ \Leftrightarrow x^2+2x-3=0\)
Xét \(a+b+c=1+2-3=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Với `x=1 => y=x^2 = 1`
Với `x=2 => y=x^2 = 4`
Vậy tọa độ giao điểm của \(\left(P\right),\left(d\right)\) là 2 điểm \(\left(1;1\right)\) và \(\left(2;4\right)\)

a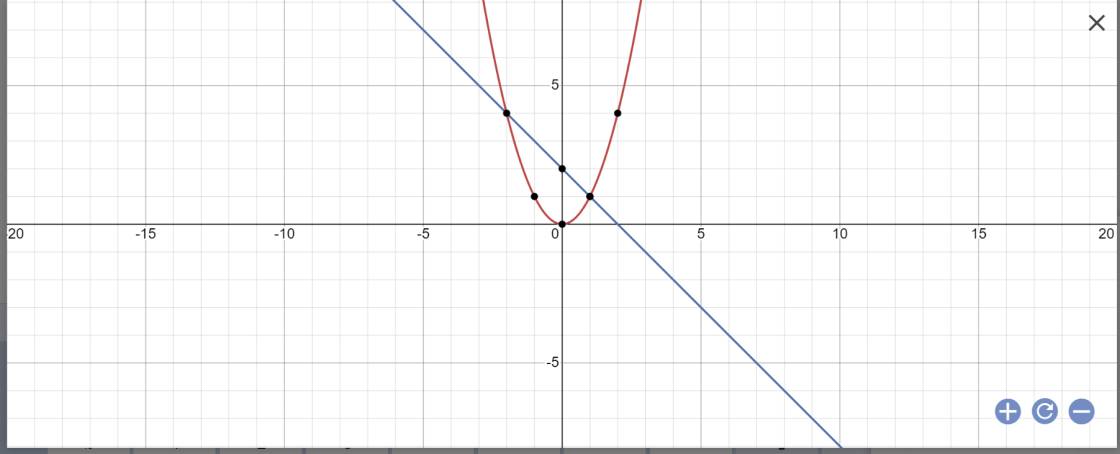
b:
PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1

b: Phương trình hoành độ giao điểm là:
\(x^2-2x-3=0\)
=>(x-3)(x+1)=0
=>x=3 hoặc x=-1
Khi x=3 thì y=9
Khi x=-1 thì y=1
Vậy: A(3;9) và B(-1;1)

a: 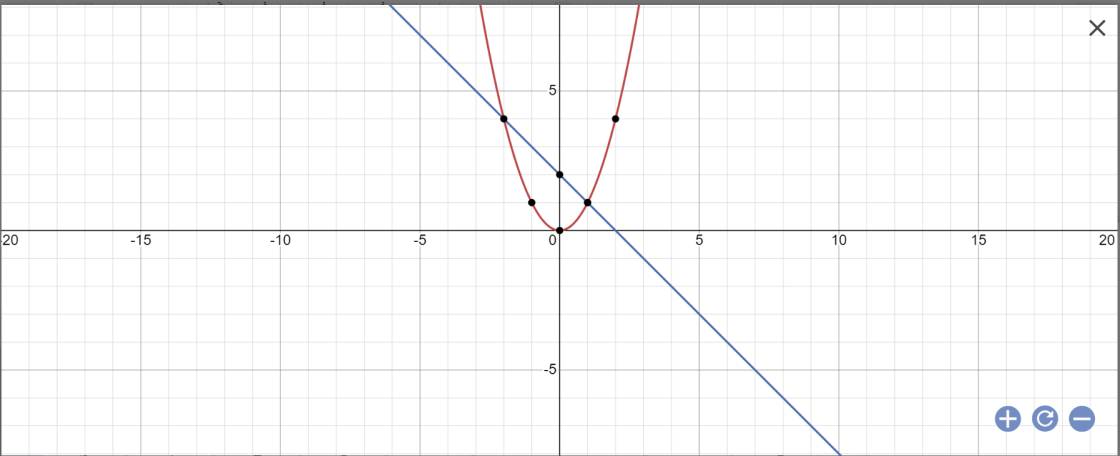
b: PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1

b) Phương trình hoành độ giao điểm là:
\(-2x^2=x-3\)
\(\Leftrightarrow-2x^2-x+3=0\)
\(\Leftrightarrow-2x^2+2x-3x+3=0\)
\(\Leftrightarrow-2x\left(x-1\right)-3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(-2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\-2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\-2x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Thay x=1 vào hàm số y=x-3, ta được:
y=1-3=-2
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=x-3, ta được:
\(x=-\dfrac{3}{2}-3=-\dfrac{9}{2}\)
Vậy: M(1;-2) và \(N\left(-\dfrac{3}{2};-\dfrac{9}{2}\right)\)

Thay x=1 vào (P), ta được:
\(y=1^2=1\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
vậy: A(1;1); B(2;4)
Gọi H là tọa độ của hình chiếu vuông góc kẻ từ O xuống AB
O(0;0); H(x;y); A(1;1); B(2;4)
\(\overrightarrow{OH}=\left(x;y\right);\overrightarrow{AB}=\left(1;3\right)\)
Vì OH vuông góc với AB nên \(x\cdot1+y\cdot3=0\)
=>x+3y=0
Ta có: \(\overrightarrow{AH}=\left(x-1;y-1\right);\overrightarrow{AB}=\left(1;3\right)\)
mà A,H,B thẳng hàng
nên \(\dfrac{x-1}{1}=\dfrac{y-1}{3}\)
=>3x-3=y-1
=>3x-y=2(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3x-y=2\\x+3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x-3y=6\\x+3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}10x=6\\x+3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\3y=-x=-\dfrac{3}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=-\dfrac{1}{5}\end{matrix}\right.\)
Vậy: \(H\left(\dfrac{3}{5};-\dfrac{1}{5}\right)\)

\(\left\{{}\begin{matrix}\left(P\right):y=x^2\\\left(d\right):y=-x+2\end{matrix}\right.\)
a) Tọa độ giao điểm của (P) và (Q) là nghiệm của hệ phương trình
\(\left\{{}\begin{matrix}y=x^2\\y=-x+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2=-x+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2+x-2=0\left(1\right)\end{matrix}\right.\)
\(pt\left(1\right)\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\) \(\left(a+b+c=1+1-2=0\right)\)
\(hpt\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2\\y=4\end{matrix}\right.\end{matrix}\right.\)
Vậy tọa độ giao điểm của (P) và (Q) là \(A\left(1;1\right)\&B\left(-2;4\right)\)
a) Phương trình hoành độ giao điểm :
x2 = - x + 2
<=> (x - 1)(x + 2) = 0
<=> \(\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Với x = 1 ta được y = 1
Với x = -2 ta được y = 4
Vậy tọa độ giao điểm là A(1; 1) ; B(-2;4)
b) Gọi C(-2 ; 0) ; D(1;0)
ta được \(S_{AOB}=S_{ABCD}-S_{BOC}-S_{AOD}\)
\(=\dfrac{\left(BC+AD\right).CD}{2}-\dfrac{BC.CO}{2}-\dfrac{AD.DO}{2}\)
\(=\dfrac{\left(4+1\right).3}{2}+\dfrac{4.2}{2}+\dfrac{1.1}{2}=12\) (đvdt)
b: Phương trình hoành độ giao điểm là:
\(x^2-2x-3=0\)
=>(x-3)(x+1)=0
=>x=3 hoặc x=-1
Khi x=3 thì y=9
Khi x=-1 thì y=1
Vậy: A(3;9)và B(-1;1)