Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{2}x^2=-\dfrac{1}{2}x-1\)
\(\Leftrightarrow-\dfrac{1}{2}x^2+\dfrac{1}{2}x+1=0\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=\dfrac{-2^2}{2}=-2\)
Thay x=-1 vào (P), ta được:
\(y=-\dfrac{1^2}{2}=-\dfrac{1}{2}\)

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2+x-2=0\\y=-x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+2\right)\left(x-1\right)=0\\y=-x+2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(-2;4\right);\left(1;1\right)\right\}\)

a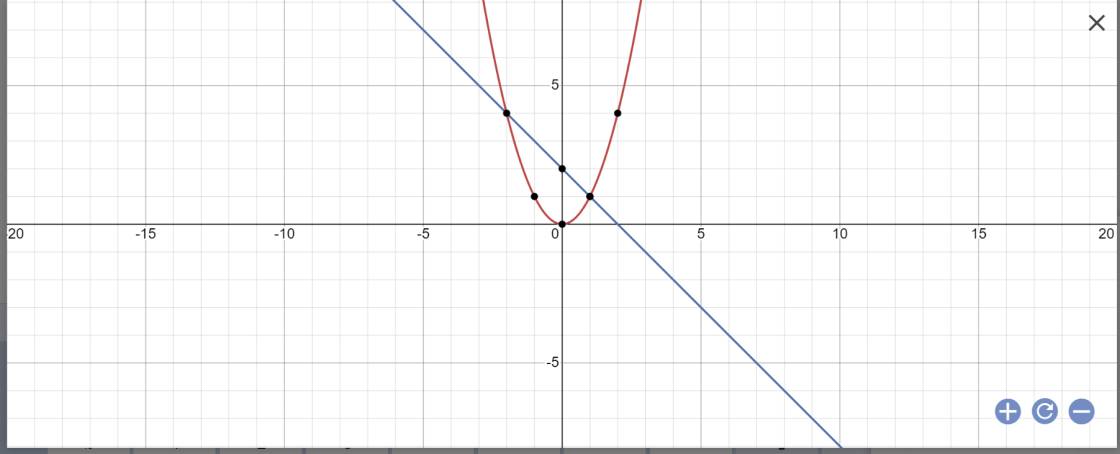
b:
PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1

a,
| -4 | -2 | 0 | 2 | 4 | |
| \(y=\frac{1}{4}x^2\) | 4 | 1 | 0 | 1 | 4 |
| \(y=-\frac{1}{2}x+2\) | 4 | 3 | 2 | 1 | 0 |
Bạn tự vẽ ha.
b,
Phương trình hoàng độ giao điểm của (p) và (d) là:
\(\frac{1}{4}x^2=-\frac{1}{2}x+2\)
\(\Leftrightarrow\frac{1}{4}x^2+\frac{1}{2}x-2=0\Leftrightarrow x^2+2x-8=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x=-4\\x=2\end{cases}}\)
\(x=-4\Rightarrow y=4\)
\(x=2\Rightarrow y=1\)
Vậy tọa độ giao điểm của (p) và (d) là (-4;4) ; (2;1)
Bạn tham khảo link này nha:
https://olm.vn/hoi-dap/detail/214561933532.html
Chúc bạn học tốt
Forever

b,
Phương trình hoàng độ giao điểm của (p) và (d) là:
1
4
x
2
=
−
1
2
x
+
2
⇔
1
4
x
2
+
1
2
x
−
2
=
0
⇔
x
2
+
2
x
−
8
=
0
⇔
(
x
+
4
)
(
x
−
2
)
=
0
⇔
\orbr
{
x
=
−
4
x
=
2
x
=
−
4
⇒
y
=
4
x
=
2
⇒
y
=
1
Vậy tọa độ giao điểm của (p) và (d) là (-4;4) ; (2;1)

1) Xác định được ít nhất hai điểm phân biệt thuộc đường thẳng d. Chẳng hạn: A ( − 3 ; 0 ) ; B ( 0 ; 3 ) .
Xác định được đỉnh và ít nhất hai điểm thuộc (P) . Chẳng hạn : O ( 0 ; 0 ) ; C ( 6 ; 9 ) ; E ( − 6 ; 9 ) .
Đồ thị
2) Phương trình hoành độ giao điểm: 1 4 x 2 = x + 3 ⇔ 1 4 x 2 − x − 3 = 0 ⇔ x = − 2 hoặc x= 6
Tọa độ giao điểm là D ( − 2 ; 1 ) v à C ( 6 ; 9 ) .

a: 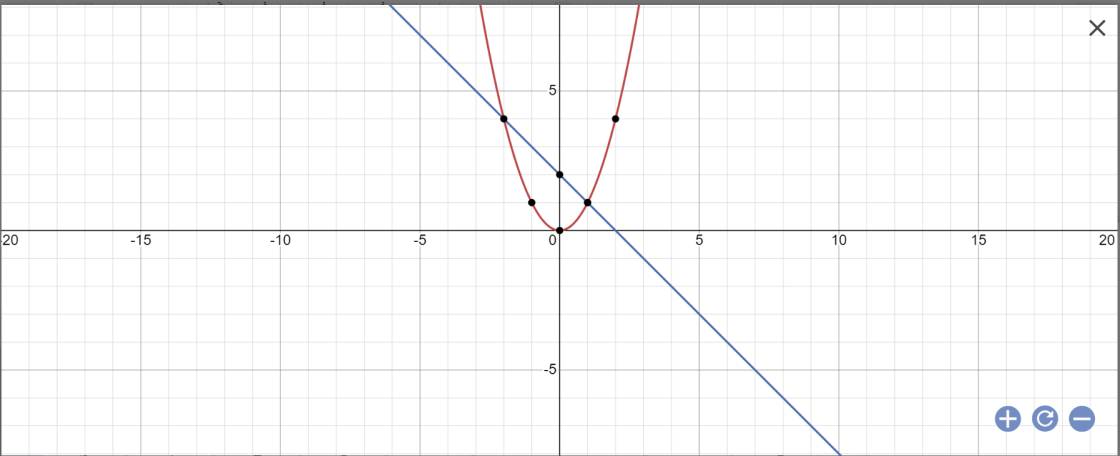
b: PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1

b: Khi m=2 thì \(y=\left(2\cdot2-1\right)x-2^2+2=3x-2\)
Phương trình hoành độ giao điểm là:
\(x^2-3x+2=0\)
=>x=2 hoặc x=1
Khi x=2 thì y=4
Khi x=1 thì y=1
c: Phương trình hoành độ giao điểm là:
\(x^2-\left(2m-1\right)x+m^2-2=0\)
\(\text{Δ}=\left(2m-1\right)^2-4\left(m^2-2\right)\)
\(=4m^2-4m+1-4m^2+8=-4m+9\)
Để (P) cắt (d) tại hai điểm phân biệt thì -4m+9>0
=>-4m>-9
hay m<9/4
a: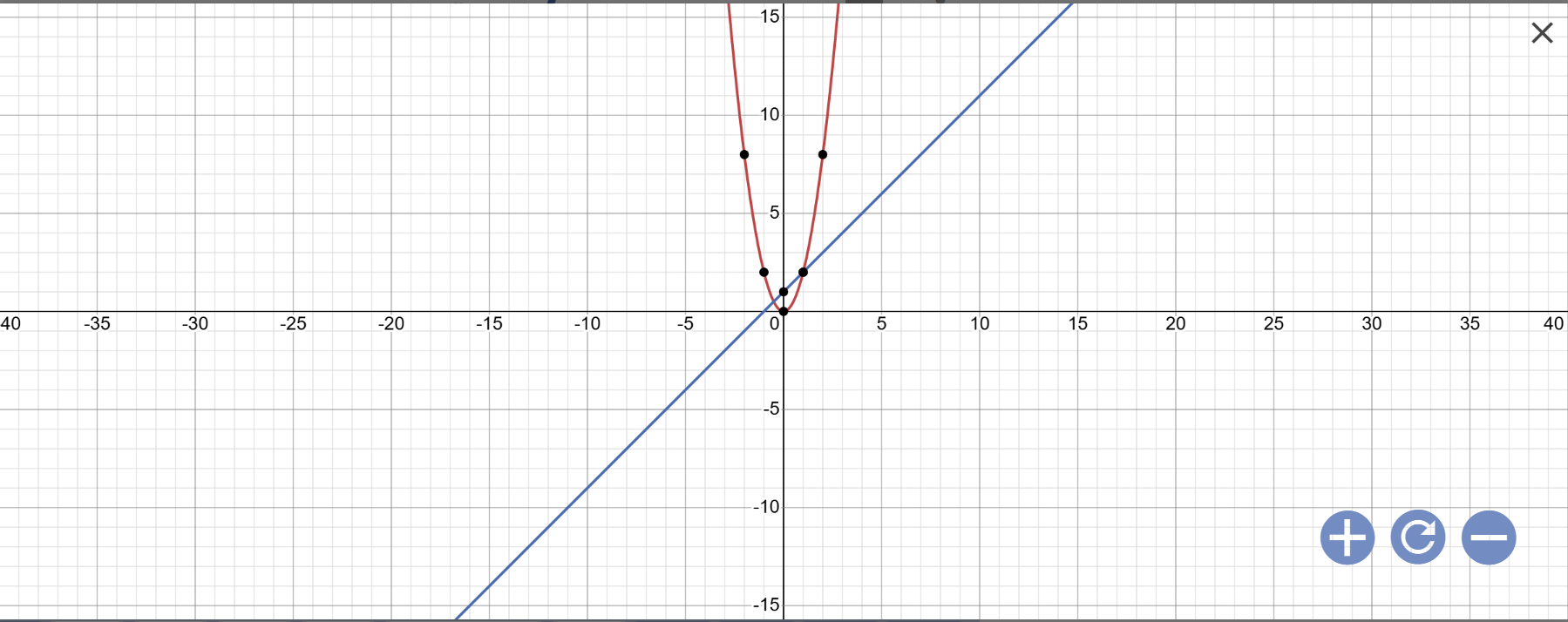
b: Phương trình hoành độ giao điểm là:
\(2x^2=x+1\)
=>\(2x^2-x-1=0\)
=>\(2x^2-2x+x-1=0\)
=>(x-1)(2x+1)=0
=>\(\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Khi x=1 thì y=x+1=1+1=2
Khi \(x=-\dfrac{1}{2}\) thì \(y=x+1=-\dfrac{1}{2}+1=\dfrac{1}{2}\)
Vậy: Tọa độ giao điểm của (d) và (P) là A(1;2); \(B\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\)