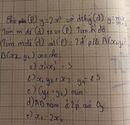Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Thay x=0 và y=9 vào (d), ta được:
\(b+6\cdot0=9\)
hay b=9
Vậy: (d): y=6x+9
b: Phương trình hoành độ giao điểm là:
\(ax^2-6x-9=0\)
\(\text{Δ}=\left(-6\right)^2-4\cdot a\cdot\left(-9\right)=36a+36\)
Để (d) tiếp xúc với (P) thì 36a+36=0
hay a=-1
`a)` Vì `(d)` đi qua `M(0;9)` nên thay `x=0` và `y=9` vào `(d)` có: `b=9`
`b)` Với `b=9=>(d):y=6x+9`
Xét ptr hoành độ của `(d)` và `(P)` có:
`ax^2=6x+9`
`<=>ax^2-6x-9=0` `(1)`
Để `(d)` tiếp xúc với `(P)` thì ptr `(1)` có nghiệm kép
`<=>\Delta' =0`
`<=>(-3)^2-a.(-9)=0`
`<=>a=-1` (t/m)

a: PTHĐGĐ là:
x^2+mx-m-2=0(1)
Khi m=2 thì (1) sẽ là
x^2+2x-2-2=0
=>x^2+2x-4=0
=>\(\left[{}\begin{matrix}x=-1+\sqrt{5}\\x=-1-\sqrt{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=6-2\sqrt{5}\\y=6+2\sqrt{5}\end{matrix}\right.\)
b: Δ=m^2-4(-m-2)
=m^2+4m+8
=(m+2)^2+4>0 với mọi x
=>(d) luôn cắt (P) tại hai điểm phân biệtx
x1^2+x2^2=7
=>(x1+x2)^2-2x1x2=7
=>(-m)^2-2(-m-2)=7
=>m^2+2m+4-7=0
=>m^2+2m-3=0
=>m=-3 hoặc m=1

Để (P) và (d) tiếp xúc với nhau thì phương trình \(\frac{-3x^2}{4}=\left(m-2\right)x+3\) có 1 nghiệm
\(\Leftrightarrow3x^2+\left(4m-8\right)x+12=0\)
Phương trình này có nghiệm kép khi:
\(\Delta'=\left(2m-4\right)^2-3.12=0\)
\(\Leftrightarrow m^2-4m-5=0\)
\(\Leftrightarrow\orbr{\begin{cases}m=5\\m=-1\end{cases}}\)
Với m = 5 thì tọa độ giao điểm là: \(\left(-2;-3\right)\)
Với m = -1 thì tọa độ giao điểm là: \(\left(2;-3\right)\)
Nghiệm kép \(\Delta=0\Rightarrow\left(m-2\right)^2-4\frac{3.}{4}.3=0\Rightarrow\)\(\hept{\begin{cases}m-2=3\\m-2=-3\end{cases}}\)
\(\hept{\begin{cases}n=5\\m=-1\end{cases}}\)

1. a, (nếu bạn cần hình vẽ thì ib mình nha)
b, MN =(d) \(\cap\) (P) là nghiệm của hệ
\(\left\{{}\begin{matrix}-2x+3=y\\x^2=y\end{matrix}\right.\)
\(\Rightarrow x^2=-2x+3\)
\(\Rightarrow\left(x-1\right)\left(x+3\right)=0\)
\(\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\) \(\left[{}\begin{matrix}y=1\\y=9\end{matrix}\right.\)
M(1;1) N(-3;9)
\(MN=\sqrt{\left(-3-1\right)^2+\left(9-1\right)^2}\)
\(=\sqrt{4^2+8^2}\)
=\(\sqrt{80}\)
2, a,
(P) và (d)+x nhau khi hệ có nghiệm
\(\left\{{}\begin{matrix}y=x^2\\y=-2x+m\end{matrix}\right.\)
\(\Leftrightarrow x^2=-2x+m\)(*)có nghiệm
\(\Leftrightarrow x^2+2x-m=0\)có nghiệm
\(\Leftrightarrow\Delta`\ge0\Leftrightarrow1-1.\left(-m\right)\ge0\)
\(\Leftrightarrow1+m\ge0\)
\(\Leftrightarrow m\ge-1\)
b, (d) và (P) cắt nhau tại 2 điểm phân biệt
\(\Leftrightarrow\)phương trình (*) có \(\Delta`\ge0\):
\(\Leftrightarrow1+m>0\)
\(\Rightarrow\)m>-1
-Chúc bạn học tốt-

a) PT hoành dộ giao điểm d và (P):
x2-mx-m-1=0 (1). \(\Delta=\left(m+2\right)^2\)
d tiếp xúc với (P) <=> m=-2 tìm được x=-1
Tọa độ điểm A(-1;1)
b) Chỉ ra (1) luôn có nghiệm x=-1; x=m+1
Điều kiện để 2 giao điểm khác phía trục tung là:m >-1
Th1: với \(\hept{\begin{cases}x_1=-1\\x_2=m+1\end{cases}}\)tìm được m=\(\frac{-10}{3}\)(loại)
Th2: Với \(\hept{\begin{cases}x_1=m+1\\x_2=-1\end{cases}}\)tìm được m=0(tm)

Lời giải:
Để $(d)$ đi qua $A(-1;-2)$ thì: $-2=-m+n(1)$
Để $(d)$ và $(P)$ tiếp xúc nhau thì PT hoành độ giao điểm:
$\frac{1}{4}x^2-mx-n=0$ có nghiệm duy nhất
Điều này xảy ra khi:
$\Delta=m^2+n=0(2)$
Từ $(1);(2)\Rightarrow m=1$ hoặc $m=-2$
Nếu $m=1$ thì $n=-1$
Nếu $m=-2$ thì $n=-4$
Vậy............

a,phương trình hoành độ giao điểm của (P) và (D) là:
x2 = mx - m + 1 (1) \(\Leftrightarrow\) x2 - mx + m - 1 = 0
\(\Delta\) = m2 - 4m +4 = (m - 20)2\(\ge\)0 với mọi giá trị của m
\(\Rightarrow\) phương trình (1) luôn luôn có nghiệm hay (D) và (P) luôn luôn có điểm chung voeí mọi giá trị của m
b,(D) tiếp xúc với (P) khi (1) có nghiệm kép hay :
\(\Delta\) = ( m - 2 )2 = 0 \(\Leftrightarrow\) m = 2
lúc đó phương trình củađường thẳng (D) là : y = 2x -1
c, tự vẽ đồ thị nha
trên đồ thị ta thấy (P) và (D) tiếp xúc nhau tại điểm A (1;1)