Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

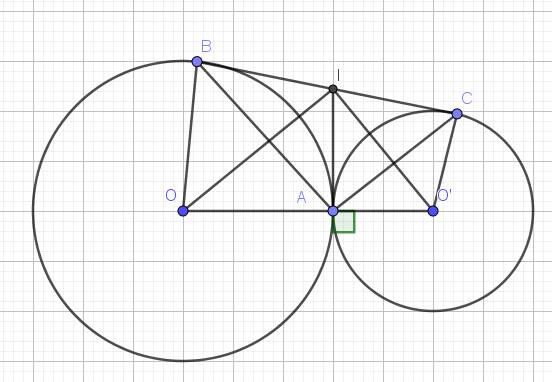
ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)

c) Xét tam giác OIO' vuông tại I, IA là đường cao có:
IA 2 = O'A.OA = 4.9 = 36 ⇒ IA = 6 cm
Lại có: BC = 2 AI ⇒ BC = 12 (cm)

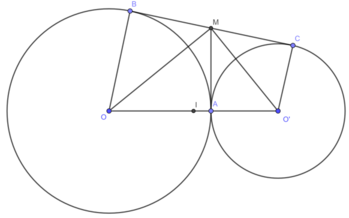
Ta có:
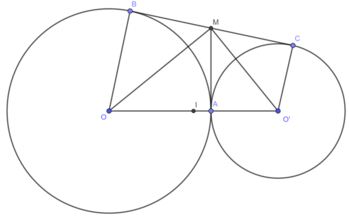
BM = MA
CM = MA
( tính chất hai tiếp tuyến cắt nhau)
⇒ BC = BM + MC = 2MA
Xét tam giác OMO’ vuông tại M có MA là đường cao.
Áp dụng hệ thức lượng trong tam giác vuông OMO’ có:
A M 2 = OM.O'M = 16.9 = 144 ⇒ AM = 12cm
⇒ BC = 2.12 = 24cm

Lời giải:
Vì $IB, IA$ là 2 tiếp tuyến giao nhau của $(O)$ nên $IB=IA$
$\Rightarrow \triangle IBA$ cân tại $I$
$\Rightarrow \widehat{IAB}=\widehat{IBA}(1)$
Tương tự: $ICA$ cân tại $I$
$\Rightarrow \widehat{IAC}=\widehat{ICA}(2)$
Từ $(1); (2)\Rightarrow \widehat{IAB}+\widehat{IAC}=\widehat{IBA}+\widehat{ICA}$
$\Rightarrow \widehat{BAC}=\widehat{CBA}+\widehat{BCA}$
Mà $\widehat{BAC}+(\widehat{CBA}+\widehat{BCA})=180^0$
$\Rightarrow \widehat{BAC}=90^0$ (đpcm)
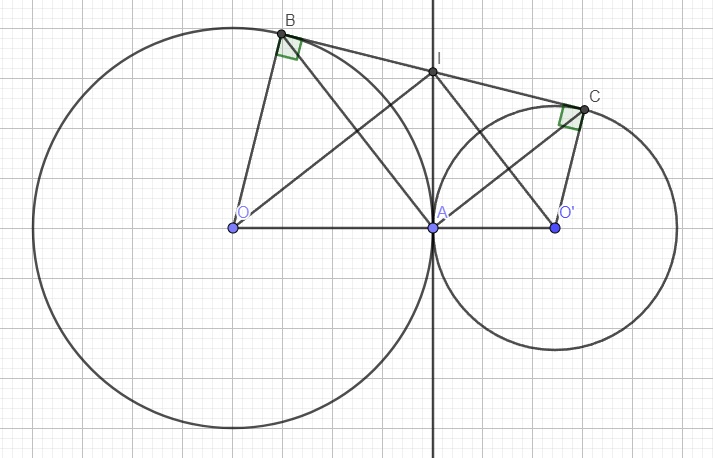
b. $(O), (O')$ tiếp xúc ngoài tại $A$ nên $O,A,O'$ thẳng hàng
$IA$ là tiếp tuyến chung của $(O), (O')$ nên $IA\perp OO'$
$BI, IA$ là 2 tiếp tuyến cắt nhau của đường tròn $(O)$ nên $IO$ là phân giác $\widehat{BIA}$ (tính chất 2 tt cắt nhau)
Tương tự: $IO'$ là phân giác $\widehat{CIA}$
Mà $\widehat{BIA}+\widehat{CIA}=\widehat{BIC}=180^0$ nên $\widehat{OIO'}=90^0$
Tam giác $OIO'$ vuông tại $I$ có $IA\perp OO'$ nên áp dụng công thức hệ thức lượng trong tam giác vuông thì:
$IA^2=OA.O'A=9.4=36$
$\Rightarrow IA=6$ (cm)
$BC=BI+IC=IA+IA=2IA=12$ (cm)

a.
Do IA và IB là tiếp tuyến của (O), theo t/c hai tiếp tuyến cắt nhau ta có: \(IA=IB\)
Tương tự, IA và IC là tiếp tuyến của (O') \(\Rightarrow IA=IC\)
\(\Rightarrow IA=IB=IC=\dfrac{1}{2}BC\)
\(\Rightarrow\Delta ABC\) vuông tại A
\(\Rightarrow\widehat{BAC}=90^0\)
b.
Theo t/c hai tiếp tuyến cắt nhau ta có:
\(\left\{{}\begin{matrix}\widehat{OIB}=\widehat{OIA}=\dfrac{1}{2}\widehat{BIA}\\\widehat{O'IC}=\widehat{O'IA}=\dfrac{1}{2}\widehat{CIA}\end{matrix}\right.\)
\(\Rightarrow\widehat{OIA}+\widehat{O'IA}=\dfrac{1}{2}\left(\widehat{BIA}+\widehat{CIA}\right)\)
\(\Rightarrow\widehat{OIO'}=\dfrac{1}{2}.\widehat{BIC}=\dfrac{1}{2}.180^0=90^0\)
\(\Rightarrow\Delta OIO'\) vuông tại O
Do IA là tiếp tuyến chung tại điểm tiếp xúc ngoài của 2 đường tròn \(\Rightarrow IA\perp O'O\)
Áp dụng hệ thức lượng trong tam giác vuông OIO' với đường cao IA:
\(IA^2=OA.O'A=36\Rightarrow IA=6\left(cm\right)\)
\(\Rightarrow BC=2IA=12\left(cm\right)\)

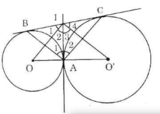
a) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.
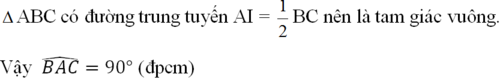
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
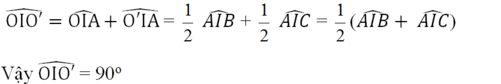
c) ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)
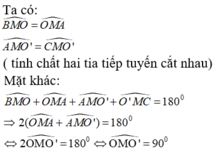
=dbfuegfnwawebfpipqpwoudqwjahfejbgfjbdsjbvjbsjfbsmajdihafbjafub cdit cmm