Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>HA=HB=AB/2
ΔOCD cân tại O
mà OK là đường cao
nên K là trung điểm của CD
=>KC=KD=CD/2
\(HA=HB=\dfrac{AB}{2}\)
\(KC=KD=\dfrac{CD}{2}\)
mà AB=CD
nên HA=HB=KC=KD
Xét (O) có
AB,CD là hai dây
AB=CD
OH,OK lần lượt là khoảng cách từ tâm O đến hai dây AB,CD
Do đó: OH=OK
Xét ΔEHO vuông tại H và ΔEKO vuông tại K có
EO chung
OH=OK
Do đó: ΔEHO=ΔEKO
b: Xét (O) có
BA,CD là hai dây
BA=CD
Do đó: BD//AC
Xét ΔEAC có BD//AC
nên \(\dfrac{EB}{BA}=\dfrac{ED}{DC}\)
mà BA=DC
nên EB=ED

a: Vì I là trung điểm của AB
và AB=2R
nên I trùng với O
=>OI=0
Ta có: ΔOCD cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)CD tại K
Ta có: K là trung điểm của CD
=>\(KC=KD=\dfrac{CD}{2}=\dfrac{R\sqrt{3}}{2}\)
Ta có: ΔOKC vuông tại K
=>\(OK^2+KC^2=OC^2\)
=>\(OK^2+\left(\dfrac{R\sqrt{3}}{2}\right)^2=R^2\)
=>\(OK^2=R^2-\left(\dfrac{R\sqrt{3}}{2}\right)^2=R^2-\dfrac{3R^2}{4}=\dfrac{1}{4}\cdot R^2\)
=>OK=1/2R
b:C1: Ta có: OI=0
OK=1/2R
=>OI<OK
C2: Xét (O) có
AB là đường kính
CD là dây
=>CD<AB
Xét (O) có
CD,AB là các dây của (O)
AB>CD
OI,OK lần lượt là khoảng cách từ O xuống AB,CD
Do đó: OI<OK
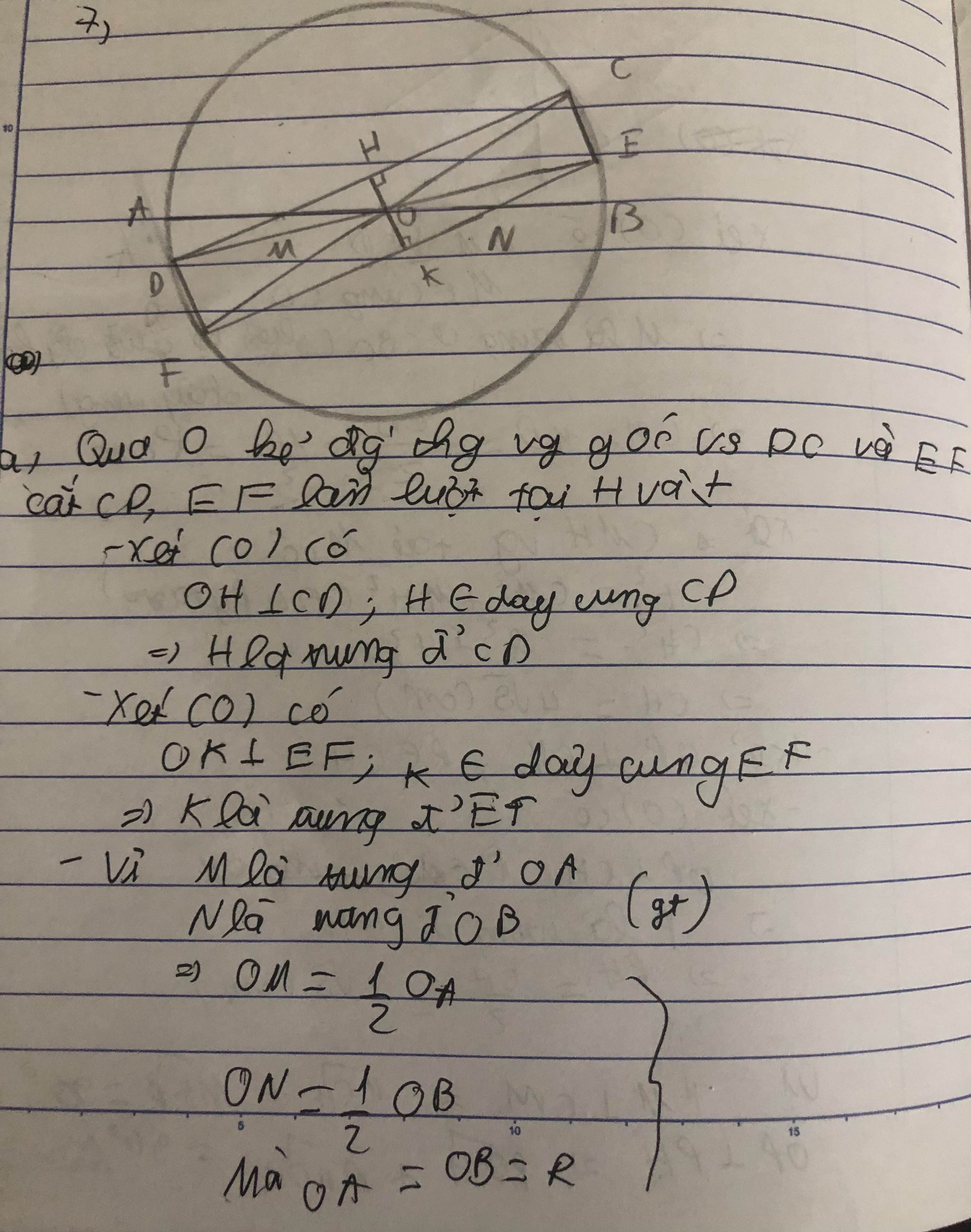


a: Xét (O) có
AB,CD là dây
AB=CD
OI là khoảng cách từ O đến AB
OK là khoảng cách từ O đến CD
Do đó: OI=OK
c: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành
=>góc BAD+góc ABC=180 độ
mà góc BAD+góc BCD=180 độ(ABCD là tứ giác nội tiếp)
nên góc ABC=góc BCD=180/2=90 độ
=>ABCD là hình chữ nhật
câu b với ạ