Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\Delta\)ABD \(\approx\)\(\Delta\)BCA ( A= B =90 ; B = C cung phụ góc BAC )
=> AB/ BC = AD/BA => AD.BC = AB2 =4R2 không đổi
b) + CM : M là trung điểm AD
MA=ME =>gocs EAM = AEM => MED = EDM ( cùng phụ EAD )
=> ME=MD =MA => M là trung điểm AD
+ tương tự N là trung ddiemr BC
* Nếu E chính giữa AB => MN//AB//DC
** E không chính giữa AB
=> Gọi AB x CD tại K ( áp dụng talet => trung tuyến KM trùng trung tuyến KN)
=> 3 đường đồng quy.
c) cô si AD+ BC >/ 2 căn AD.BC = 2R
=> S min =AB .(AD+BC) /2 = 2R.R = 2R2
khi AD =BC ( E chính giữa AB)
tự trình bày cho rõ nhé..

a: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB
Ta có: CM+MD=CD
nên CA+DB=CD

C là giao điểm 2 tiếp tuyến tại A và M \(\Rightarrow OC\) là trung trực AM
\(\Rightarrow E\) là trung điểm AM
Tương tự ta có OD là trung trực BM \(\Rightarrow F\) là trung điểm BM
\(\Rightarrow EF\) là đường trung bình tam giác ABM
\(\Rightarrow EF||AB\Rightarrow ONEF\) là hình thang (1)
Lại có O là trung điểm AB \(\Rightarrow OF\) là đường trung bình tam giác ABM
\(\Rightarrow OF=\dfrac{1}{2}AM=AE\)
Mà \(OF||AE\) (cùng vuông góc BM)
\(\Rightarrow AEFO\) là hình bình hành \(\Rightarrow\widehat{OFE}=\widehat{OAE}\)
Mà \(EN=AE=\dfrac{1}{2}AM\Rightarrow\Delta AEN\) cân tại E \(\Rightarrow\widehat{OAE}=\widehat{ANE}\)
\(\widehat{ANE}+\widehat{ONE}=180^0\Rightarrow\widehat{OFE}+\widehat{ONE}=180^0\)
Lại có \(\widehat{ONE}+\widehat{NEF}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{OFE}=\widehat{NEF}\)
\(\Rightarrow ONEF\) là hình thang cân
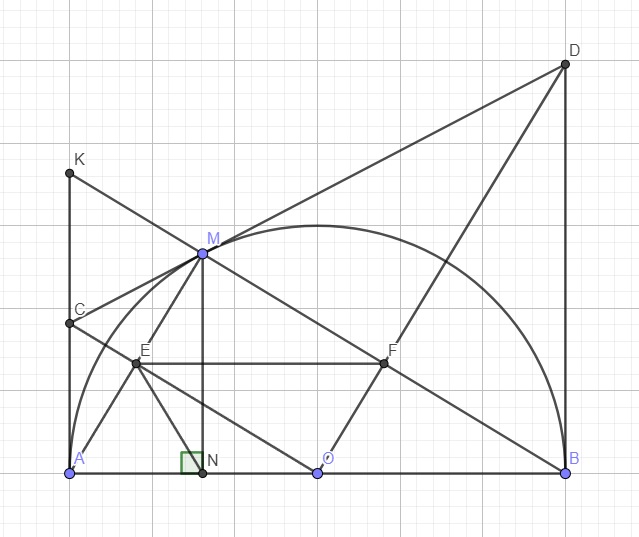

Gọi AB giao MN là T
MN giao CD là K
Tam giác TAM đồng dạng TBN
KMD đồng dạng KNC
=>\(\frac{TA}{TB}=\frac{TM}{TN}=\frac{KM}{KN}=\frac{KD}{KC}=\frac{AD}{BC}\)
M,N cố định => K trùng T => đpcm