Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, 700 góc nào bạn ?
b, Vì AB là tiếp tuyến (O) => ^ABO = 900
AO giao BC = K
AB = AC ; OB = OC = R
Vậy OA là đường trung trực đoạn BC
Xét tam giác ABO vuông tại B, đường cao BK
Áp dụng định lí Pytago tam giác ABO vuông tại B
\(AB=\sqrt{AO^2-BO^2}=\sqrt{16-4}=2\sqrt{3}\)cm
Áp dụng hệ thức : \(BK.AO=BO.AB\Rightarrow BK=\frac{BO.AB}{AO}=\frac{4\sqrt{3}}{4}=\sqrt{3}\)cm
Vì AO là đường trung trực => \(BC=2KB=2\sqrt{3}\)cm
Chu vi tam giác ABC là :
\(P_{ABC}=AB+AC+BC=2AB+BC=4\sqrt{3}+2\sqrt{3}=6\sqrt{3}\)cm

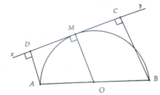
Ta có ABCD là hình thang vuông tại C và D
Mà O Là trung điểm AB và OM vuông góc với CD( tiếp tuyến của (O)
=> AD+BC=2OM=2R. Chú ý rằng CD ≤ AB (hình chiếu đường xiên)
=> S A B C D = 1 2 A D + B C . C D
= R.CD ≤ R.AB = 2 R 2
Do đó S A B C D lớn nhất khi CD=AB hay M là điểm chính giữa nửa đường tròn đường kính AB

a/ Ta có : \(\hept{\begin{cases}AH\text{//}OM\text{//}BK\\OA=OB\end{cases}}\) \(\Rightarrow\)OM là đường trung bình của hình thang ABKH
\(\Rightarrow\)\(AH+BK=2OM=2R\) (không đổi)
b/ Từ M hạ MN vuông góc với AB tại N (1)
Ta sẽ chứng minh MN = MK
Xét trong (O;R) thì : \(\widehat{BMK}=\widehat{MAB}\) (cùng chắn cung MB)
Mà : \(\hept{\begin{cases}\widehat{BMK}+\widehat{MBK}=90^o\\\widehat{MAB}+\widehat{MBA}=90^o\end{cases}}\) \(\Rightarrow\)\(\widehat{MBA}=\widehat{MBK}\)
Xét hai tam giác vuông NBM và KBM có MB là cạnh huyền (chung) , \(\widehat{MBA}=\widehat{MBK}\)
\(\Rightarrow\)\(\Delta NBM=\Delta KBM\) (ch.gn)
\(\Rightarrow\) MN = MK (2)
Từ (1) và (2) suy ra đpcm.
c/ Vì ABKH là hình thang vuông nên \(S_{ABKH}=\frac{1}{2}\left(AH+BK\right).HK=\frac{1}{2}.2OM.HK\)
\(=\left(2MN\right).OM\) . Mà OM = R không đổi, vậy \(maxS_{ABKH}\Leftrightarrow maxMN\Leftrightarrow MN=OM\)\(\Leftrightarrow\)M là điểm chính giữa cung AB
Khi đó thì : \(S_{ABKH}=2OM.OM=2R^2\)

a/ Dễ dàng chứng minh được OA chính là đường trung bình của hình thang HBCK, suy ra A là trung điểm HK => A chính là tâm của đường tròn đường kính HK.
Để chứng minh đường tròn đường kính HK tiếp xúc với BC, ta sẽ chứng minh BC chính là tiếp tuyến của đường tròn (A) tại M hay AM = AK.
Vì HK là tiếp tuyến của (O) tại A nên : \(\widehat{CAK}=\frac{1}{2}\text{sđcungAC}=\widehat{ABC}\left(1\right)\)
Mặt khác, tam giác BAC vuông tại A vì cạnh huyền BC là đường kính của đường tròn (O) . Ta dễ dàng suy ra \(\widehat{ABC}=\widehat{CAM}\left(2\right)\)
Từ (1) và (2) ta có \(\widehat{CAK}=\widehat{CAM}\)
Xét hai tam giác vuông CAM và tam giác vuông CAK có CA là cạnh chung , góc CAM = góc CAK nên \(\Delta CAK=\Delta CAM\left(ch.gn\right)\Rightarrow AK=AM\)
Từ đó suy ra đpcm.
b/ Vì BHKC là hình thang nên \(S_{BHKC}=\frac{\left(BH+CK\right).HK}{2}=OA.HK\)
Từ câu a) ta chứng minh được \(AK=AM\) nên \(HK=2AK=2AM\le2OA\) (hằng số)
=>\(S_{BHKC}\le OA.2OA=2OA^2=2\left(\frac{BC}{2}\right)^2=\frac{BC^2}{2}\) . Dấu "=" xảy ra khi A là điểm chính giữa cung BC.
Vậy ...............................
c/ Đề sai , bởi vì góc MAO có đơn vị độ, còn vế bên phải lại là một tỉ số .
@Hoàng Lê Bảo Ngọc
bn xem có phải k sao cô minh cho đề thế nhỉ

a,
- Vì M,N lần lượt là hình chiếu của A và B trên d (gt) nên ta có
AM và BN cùng vuông góc với d
=> AM song song BN
- Xét tứ giác AMNB có:
AM song song BN(cmt)
=> AMNB là hình thang mà góc AMN = 90* ( AM vuông góc MN)
=> tg AMNB là hình thang vuông.
Vậy...
CÓ AI CÒN ON KHÔNG