Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Dễ thấy C là trực tâm của tam giác IAB nên C, I, H thẳng hàng.
Do tứ giác AICK là hình thang nội tiếp được đường tròn nên là hình thang cân.
Khi đó \(\widehat{IAK}=\widehat{CKA}\Rightarrow\widehat{IAB}=\widehat{NBA}\)
Suy ra tam giác NAB vuông cân tại N nên \(\widehat{NBA}=45^o\).
Ta có các tứ giác CMIN, AMIH nội tiếp được nên \(\widehat{NMH}=\widehat{NMI}+\widehat{HMI}=\widehat{ICN}+\widehat{IAB}=45^o+45^o=90^o\Rightarrow MN\perp MH\).

c) Đề phải là \(\dfrac{IC}{IH}+\dfrac{IA}{IN}+\dfrac{IB}{IM}\ge6\).
Đặt \(x=\dfrac{IH}{CH};y=\dfrac{IN}{AN};z=\dfrac{IM}{BM}\left(x,y,z< 1\right)\).
Ta có \(x+y+z=\dfrac{S_{IAB}}{S_{ABC}}+\dfrac{S_{IBC}}{S_{ABC}}+\dfrac{S_{ICA}}{S_{ABC}}=1\).
Lại có \(\dfrac{IH}{CH}=x\Rightarrow\dfrac{CH}{IH}=\dfrac{1}{x}\Rightarrow\dfrac{IC}{IH}=\dfrac{1}{x}-1\).
Tương tự \(\dfrac{IA}{IN}=\dfrac{1}{y}-1;\dfrac{IB}{IM}=\dfrac{1}{z}-1\).
Do đó \(\dfrac{IC}{IH}+\dfrac{IA}{IN}+\dfrac{IB}{IM}=\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}-3\ge_{Svacxo}\dfrac{9}{x+y+z}-3=\dfrac{9}{1}-3=6\).
Vậy ta có đpcm.

1:
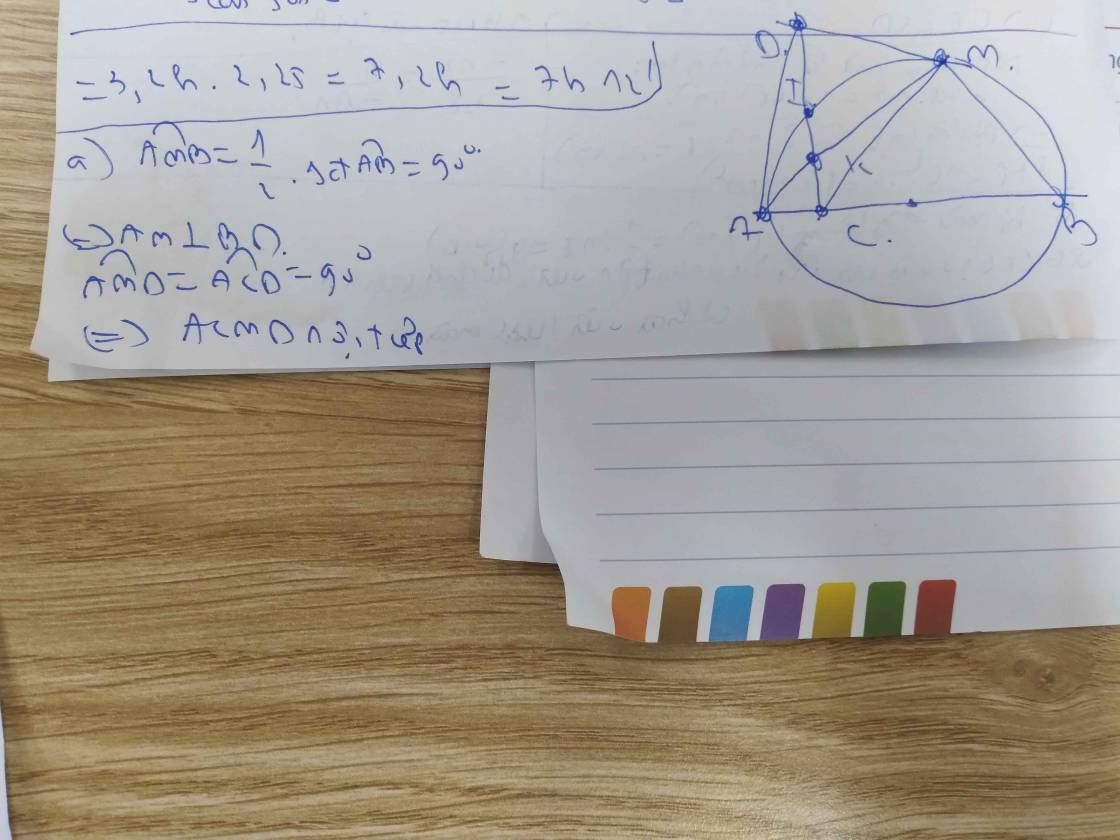
góc AMB=1/2*sđ cung AB=90 độ
=>AM vuông góc BD
góc ACD=góc AMD=90 độ
=>ACMD nội tiếp
góc KCB+góc KMB=180 độ
=>BMKC nội tiếp
2: Xét ΔCAK vuông tại C và ΔCDB vuông tại C có
góc CAK=góc CDB
=>ΔCAK đồng dạng với ΔCDB
=>CA/CD=CK/CB
=>CA*CB=CD*CK