Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Gọi I là trung điểm của CD
Xét hình thang ACDB (AC//BD) có:\(\hept{\begin{cases}CI=ID\\AO=BO\end{cases}}\)
=>OI là đường tung bình của hình thang ACDB
=>\(OI=\frac{AC+BD}{2}=\frac{CD}{2}=CI=DI\)
=>Tam giác COD vuông tại O
=> đpcm
b)Kẻ OE vuông góc với CD,giao cuae CO và BD là F
Ta có tam giác ACO=Tam giác BFO( cạnh góc vuông-góc nhọn kề)
=>OC=OF
Xét tam giác CDF có:
CO=OF (cmt)
DO vuông góc với CF
=>tam giác CDF cân tại D
=>DO là phân giác góc CDF
=>góc EDO=BDO
=>tam giác EOD=tam giác BOD(Cạnh huyền - góc nhọn)
=>OE=OB
=>EO là bán kính (O) mà OE vuông góc với BC(cách vẽ)
=>CD là tiếp tuyến đường tròn đường kính AB

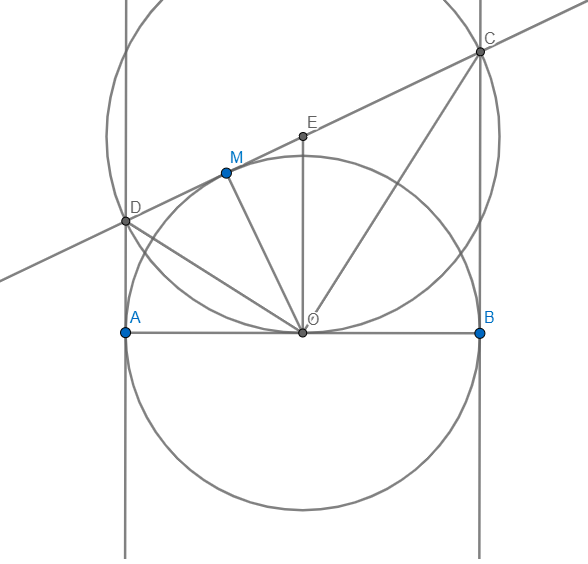
b) Vì DA,DM là tiếp tuyến \(\Rightarrow OD\) là phân giác \(\angle MOA\)
\(\Rightarrow\angle MOD=\dfrac{1}{2}\angle MOA\)
Vì CB,CM là tiếp tuyến \(\Rightarrow OC\) là phân giác \(\angle MOB\)
\(\Rightarrow\angle MOC=\dfrac{1}{2}\angle MOB\)
\(\Rightarrow\angle MOC+\angle MOD=\dfrac{1}{2}\left(\angle MOA+\angle MOB\right)\)
\(\Rightarrow\angle COD=\dfrac{1}{2}\angle AOB=\dfrac{1}{2}.180=90\)
c) Vì \(\angle COD=90\Rightarrow O\in\) đường tròn đường kính CD
Gọi E là tâm đường tròn đường kính CD \(\Rightarrow E\) là trung điểm CD
Ta có: E là trung điểm CD,O là trung điểm AB và ABCD là hình thang
\(\Rightarrow EO\parallel AD\) \(\Rightarrow EO\bot AB\Rightarrow AB\) là tiếp tuyến của đường tròn đường kính CD


a: Xét (O) có
DC,DA là tiếp tuyến
=>DC=DA và OD là phân giác của góc COA
=>OD vuông góc AC
Xét (O) có
EC,EB là tiếp tuyến
=>EB=EC và OE là phân giác của góc COB(2)
=>OE là trung trực của BC
=>OE vuông góc CB
AD+BE=DC+CE=DE
b: Từ (1), (2) suy ra góc DOE=1/2*180=90 độ
Xét tứ giác CMON có
góc CMO=góc CNO=góc MON=90 độ
=>CMON là hình chữ nhật
c: OM*OD+ON*OE
=OC^2+OC^2
=2*R^2ko đổi
ko biết vì chỉ đang học lớp 7 thui nha, ko biết để mà giúp
tui mới học lớp 8 .chưa học đường tròn.ko giúp được.sorry nha