Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

░░░░░░░░░░░░▄▄
░░░░░░░░░░░█░░█
░░░░░░░░░░░█░░█
░░░░░░░░░░█░░░█
░░░░░░░░░█░░░░█
███████▄▄█░░░░░██████▄
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█████░░░░░░░░░█
██████▀░░░░▀▀█████
k mk đi mk k lại cho

a) Xét (O) có
ΔABC nội tiếp đường tròn(A,B,C∈(O))
AB là đường kính của (O)
Do đó: ΔABC vuông tại C(Định lí)
⇒BC⊥AC tại C
⇒BC⊥AE tại C
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAE vuông tại B có BC là đường cao với cạnh huyền AE, ta được:
\(AC\cdot AE=AB^2\)
mà AB không đổi(Do AB là đường kính của (O))
nên \(AC\cdot AE\) không đổi(đpcm)
b) Xét (O) có
ΔADB nội tiếp đường tròn(A,D,B∈(O))
AB là đường kính của (O)(gt)
Do đó: ΔADB vuông tại D(Định lí)
⇒BD⊥AD tại D
⇒BD⊥AF tại D
Xét ΔABD vuông tại D và ΔAFB vuông tại B có
\(\widehat{DAB}\) chung
Do đó: ΔABD∼ΔAFB(g-g)
⇒\(\widehat{ABD}=\widehat{AFB}\) (hai góc tương ứng)
hay \(\widehat{ABD}=\widehat{DFB}\)(đpcm)
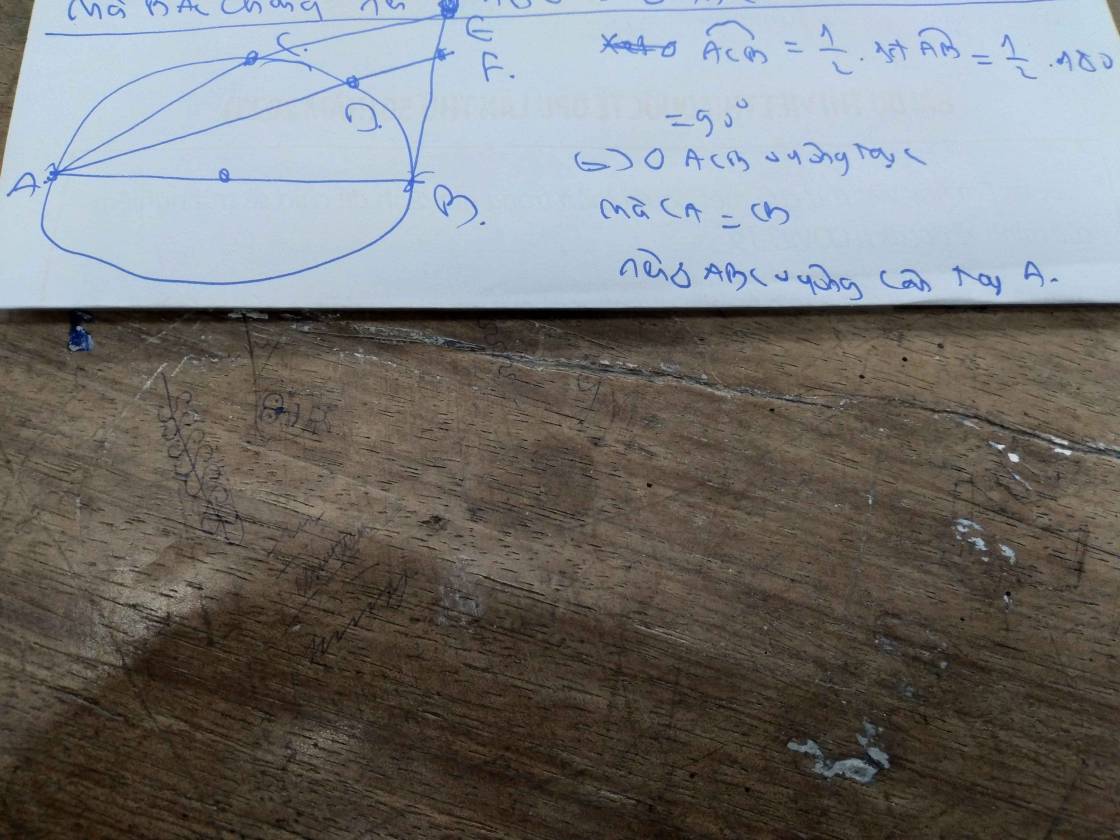
cho nua duong tron tam o duong kinh AB , ke tiep tuyen Bx va lay hai diem C va D thuoc nua duong tron , cac tia AC va AD cat Bx lan luot o E, F ( F o giua B va E) ,1, chung minh rang ABD=DFB ,2, chung minh rang CEFD la tu guac noi tiep /

b: Xét ΔBHA có
BD vừa là đường cao, vừa là phân giác
=>ΔBHA cân tại B
=>D là trung điểm của AH
góc EAD=1/2*sđ cung AD
góc FAD=góc FBC=1/2*sđ cung DC
mà sđ cung AD=sđ cung DC
nên góc EAD=góc FAD
=>AD là phân giác của góc EAF
=>D là trung điểm của EF
Xét tứ giác AEHF có
D là trung điểm chung của AH và EF
AH vuông góc EF
=>AEHF là hình thoi
a: góc ADB=1/2*180=90 độ
=>BD vuông góc AH
góc ACB=1/2*180=90 độ
=>AC vuông góc HB
góc HDF+góc HCF=180 độ
=>HDFC nội tiếp