Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn xem lại đề nhé! Hình như có gì đó sai sai....

a) Xét \(\Delta PIM;\Delta PIN\) có :
\(PM=PN\) (tam giác MNP cân tại P)
\(\widehat{MPI}=\widehat{NPI}\) (PI là tia phân giác của \(\widehat{MPN}\) )
\(PI:chung\)
=> \(\Delta PIM=\Delta PIN\left(c.g.c\right)\)
*Cách khác :
Xét \(\Delta PIM;\Delta PIN\) có :
\(\widehat{PMI}=\widehat{PNI}\) (tam giác MNP cân tại P)
\(PM=PN\)(tam giác MNP cân tại P)
\(\widehat{MPI}=\widehat{NPI}\) (PI là tia phân giác của góc MPN)
=> \(\Delta PIM=\Delta PIN\left(g.c.g\right)\)
b) Xét \(\Delta PEI;\Delta PFI\) có :
\(\widehat{PEI}=\widehat{PFI}\left(=90^{^O}\right)\)
\(PI:Chung\)
\(\widehat{EPI}=\widehat{FPI}\left(cmt\right)\)
=> \(\Delta PEI=\Delta PFI\) (cạnh huyền - góc nhọn)
=> \(IE=IF\) (2 cạnh tương ứng)
c) Ta chứng minh được \(\Delta PIK=\Delta PIH\left(g.c.g\right)\)
Suy ra : \(PK=PH\) (2 cạnh tương ứng)
Xét \(\Delta PHK\) có :
\(PK=PH\left(cmt\right)\)
=> \(\Delta PHK\) cân tại P (đpcm)
d) Xét \(\Delta PEF\) cân tại E có :
\(\widehat{PEF}=\widehat{PFE}=\dfrac{180^o-\widehat{P}}{2}\left(1\right)\)
Xét \(\Delta PKH\) cân tại P (cmt) có :
\(\widehat{PKH}=\widehat{PHK}=\dfrac{180^o-\widehat{P}}{2}\left(2\right)\)
Từ (1) và (2) => \(\widehat{PEF}=\widehat{PKH}\left(=\dfrac{180^o-\widehat{P}}{2}\right)\)
Mà thấy : 2 góc này đều ở vị trí đồng vị
=> \(\text{EF // HK (đpcm)}\)

Sửa đề: IE vuông góc với PM, IF vuông góc với PN
a: Xét ΔPIM và ΔPIN có
PI chung
\(\widehat{MPI}=\widehat{NPI}\)
PM=PN
Do đó: ΔPIM=ΔPIN
b: Xét ΔPEI vuông tạiE và ΔPFI vuông tại F có
PI chung
\(\widehat{EPI}=\widehat{FPI}\)
Do đó: ΔPEI=ΔPFI
Suy ra: IE=IF

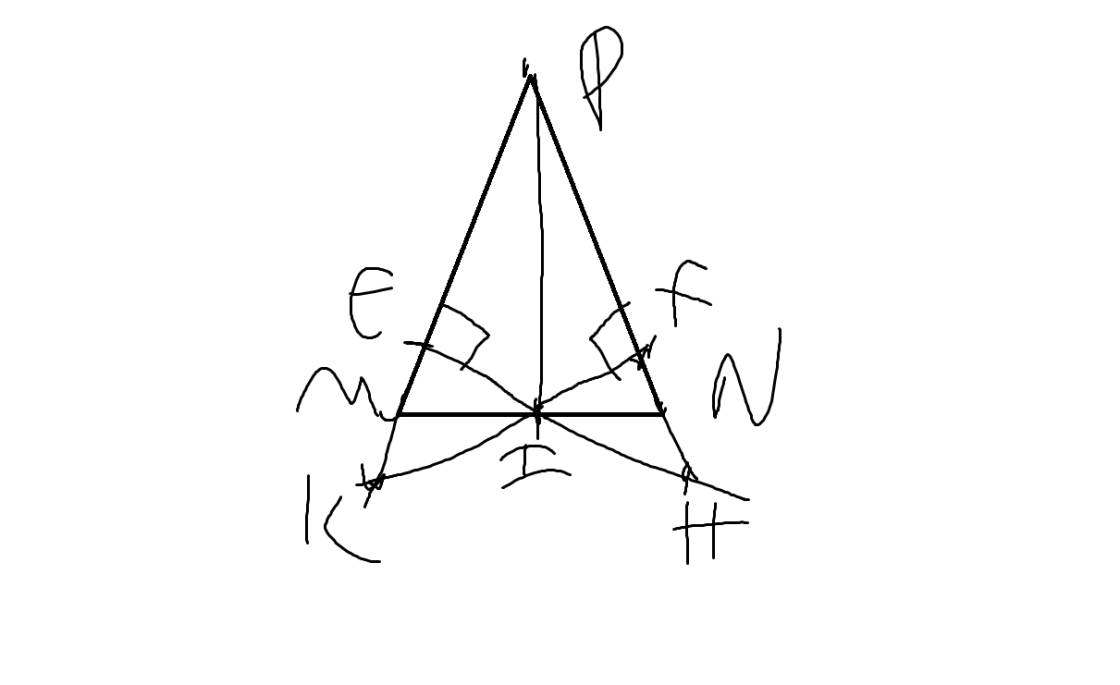
a: Xét ΔPIM và ΔPIN có
PM=PN
\(\widehat{MPI}=\widehat{NPI}\)
PI chung
Do đó: ΔPIM=ΔPIN
b: Xét ΔPEI vuông tại E và ΔPFI vuông tại F có
PI chung
\(\widehat{EPI}=\widehat{FPI}\)
Do đó: ΔPEI=ΔPFI
=>IE=IF
c: Xét ΔIEK vuông tại E và ΔIFH vuông tại F có
IE=IF
\(\widehat{EIK}=\widehat{FIH}\)(hai góc đối đỉnh)
Do đó: ΔIEK=ΔIFH
=>EK=FH
Ta có: PE+EK=PK
PF+FH=PH
mà PE=PF(ΔPEI=ΔPFI)
và EK=FH
nên PK=PH
=>ΔPHK cân tại P
d: Xét ΔPKH có \(\dfrac{PE}{PK}=\dfrac{PF}{PH}\)
nên EF//HK
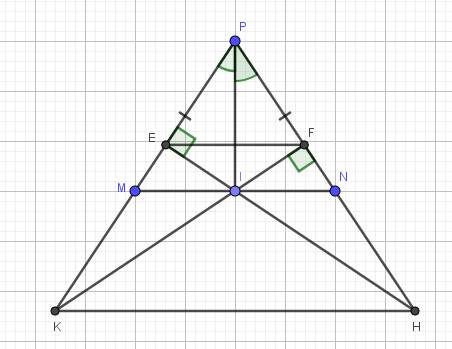
a) Do \(\Delta MNP\) cân tại P (gt)
\(\Rightarrow PM=PN\)
Do PI là tia phân giác của \(\widehat{MPN}\) (gt)
\(\Rightarrow\widehat{MPI}=\widehat{NPI}\)
Xét \(\Delta PIM\) và \(\Delta PIN\) có:
\(PM=PN\) (cmt)
\(\widehat{MPI}=\widehat{NPI}\) (cmt)
\(PI\) là cạnh chung
\(\Rightarrow\Delta PIM=\Delta PIN\left(c-g-c\right)\)
b) Do \(\widehat{MPI}=\widehat{NPI}\left(cmt\right)\)
\(\Rightarrow\widehat{EPI}=\widehat{FPI}\)
Xét hai tam giác vuông: \(\Delta EPI\) và \(\Delta FPI\) có:
PI là cạnh chung
\(\widehat{EPI}=\widehat{FPI}\) (cmt)
\(\Rightarrow\Delta EPI=\Delta FPI\) (cạnh huyền - góc nhọn)
\(\Rightarrow IE=IF\) (hai cạnh tương ứng)
c) Do \(\Delta EPI=\Delta FPI\) (cmt)
\(\Rightarrow PE=PF\) (hai cạnh tương ứng)
Xét hai tam giác vuông: \(\Delta IEK\) và \(\Delta IFH\) có:
\(IE=IF\left(cmt\right)\)
\(\widehat{EIK}=\widehat{FIH}\) (đối đỉnh)
\(\Rightarrow\Delta IEK=\Delta IFH\) (cạnh góc vuông - góc nhọn kề)
\(\Rightarrow EK=FH\) (hai cạnh tương ứng)
Mà \(PE=PF\left(cmt\right)\)
\(\Rightarrow EK+PE=FH+PF\)
\(\Rightarrow PK=PH\)
\(\Rightarrow\Delta PHK\) cân tại P
d) Do \(\Delta PHK\) cân tại P (cmt)
\(\Rightarrow\widehat{PKH}=\widehat{PHK}=\dfrac{180^0-\widehat{MPN}}{2}\) (1)
Do PE = PF (cmt)
\(\Rightarrow\Delta PEF\) cân tại P
\(\Rightarrow\widehat{PEF}=\widehat{PFE}=\dfrac{180^0-\widehat{MPN}}{2}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{PKH}=\widehat{PEF}\)
Mà \(\widehat{PKH}\) và \(\widehat{PEF}\) là hai góc đồng vị
\(\Rightarrow EF\) // \(HK\)
a) Xét ΔPIM và ΔPIN có
PM=PN(do ΔMPN cân tại B)
\(\widehat{MPI}=\widehat{NPI}\)(do PI là tia phân giác của \(\widehat{MPN}\))
PI là cạnh chung
Do đó: ΔPIM=ΔPIN(c-g-c)
b)Ta có: ΔPIM=ΔPIN(cmt)
⇒MI=IN(hai cạnh tương ứng)
Xét ΔIEM vuông tại E và ΔIFN vuông tại F có
MI=IN(cmt)
\(\widehat{EMI}=\widehat{FNI}\)(hai góc ở đáy của ΔPMN cân tại P)
Do đó: ΔIEM=ΔIFN(cạnh huyền-góc nhọn)
⇒IE=IF(hai cạnh tương ứng)
c) Xét ΔIEK vuông tại E và ΔIFH vuông tại F có
EI=IF(cmt)
\(\widehat{EIK}=\widehat{FIH}\)(hai góc đối đỉnh)
Do đó: ΔIEK=ΔIFH(cạnh góc vuông-góc nhọn kề)
⇒EK=FH(hai cạnh tương ứng)(1)
Ta có: EK=EM+MK(do E,M,K thẳng hàng)(2)
FH=FN+NH(do F,N,H thẳng hàng)(3)
Từ (1) , (2) và (3) suy ra EM+MK=FN+NH
mà EM=FN(ΔIEM=ΔIFN)
nên MK=NH
Ta có: PK=PM+MK(do P,M,K thẳng hàng)
PH=PN+NH(do P,N,H thẳng hàng)
mà PM=PN(do ΔPMN cân tại P)
và MK=NH(cmt)
nên PK=PH
Xét ΔPKH có PK=PH(cmt)
nên ΔPKH cân tại P(đ/n tam giác cân)
d) Xét ΔPEI vuông tại E và ΔPFI vuông tại F có
PI là cạnh chung
\(\widehat{EPI}=\widehat{FPI}\)(PI là tia phân giác của \(\widehat{EPF}\))
Do đó: ΔPEI=ΔPFI(cạnh huyền-góc nhọn)
⇒PE=PF(hai cạnh tương ứng)
Xét ΔPEF có PE=PF(cmt)
nên ΔPEF cân tại P(định nghĩa tam giác cân)
⇒\(\widehat{PEF}=\frac{180^0-\widehat{P}}{2}\)(số đo một góc ở đáy của ΔPEF cân tại P)(4)
Ta có: ΔPKH cân tại P(cmt)
⇒\(\widehat{PKH}=\frac{180^0-\widehat{P}}{2}\)(số đo một góc ở đáy của ΔPKH cân tại P)(5)
Từ (4) và (5) suy ra \(\widehat{PEF}=\widehat{PKH}\)
mà \(\widehat{PEF}\) và \(\widehat{PKH}\) là hai góc ở vị trí đồng vị
nên EF//HK(dấu hiệu nhận biết hai đường thẳng song song)(đpcm)
Hình vẽ.