Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

nua chu vi là: 60 : 2= 30 cm
tong so phan bang nhau cua CD va CR la: 3 + 2 = 5
CR: 30 : 5 x 2= 12 cm
CD 30: 5 X 3= 18 cm
a, DTHCN: 12 x 18 = .........
b. Ve hình sẽ thấy
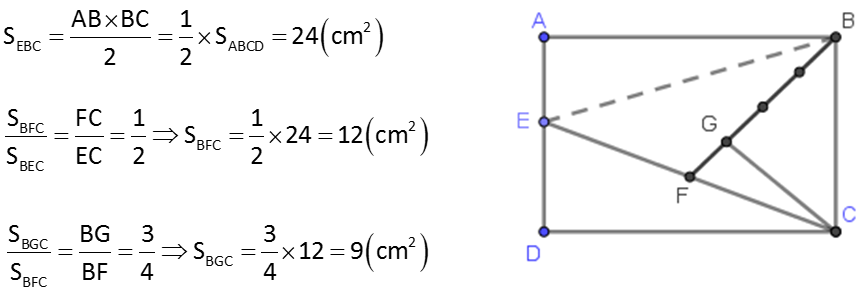
hai tam giác có cùng chieu cao là CE
canh BM = 2 MC nên DT.MBE = 2 DT .MCD
nua chu vi la :60:2=30(cm)
tong so phan bang nhau la :3+2=5
chieu dai la 30:5*3=18(cm)
chieu rong la :18*\(\frac{2}{3}\)=12(cm)
SABCD la: 12*18=216(cm2)
b, vi MB=2MC nen MEB=2MCD

a ) Chiều dài hình chữ nhật ABCD là :
60 : 2 : ( 3 + 2 ) x 3 = 18 ( cm )
Chiều rộng hình chữ nhật ABCD là :
60 : 2 : ( 3 + 2 ) x 2 = 12 ( cm )
Diện tích hình chữ nhật ABCD là :
18 x 12 = 216 ( cm2 )
b ) Diện tích tam giác ABE là :
18 x 12 : 2 = 108 ( cm2 )
Diện tích tam giác ABM là :
18 x ( 12 : 3 x 2 ) : 2 = 72 ( cm2 )
Vậy diện tích tam giác MBE là :
108 - 72 = 36 ( cm2 )
Diện tích tam giác MCD là :
18 x ( 12 - 8 ) : 2 = 36 ( cm2 )
Vậy diện tích tam giác MBE bằng diện tích tam giác MCD .
c ) EC là đường cao ứng với cạnh đáy BM của tam giác BME .
Vậy EC bằng :
36 x 2 : 8 = 9 ( cm )
Diện tích tam giác ADE bằng :
12 x ( 18 + 9 ) : 2 = 162 ( cm2 )
Xét hai tam giác ABE và ADE có cùng cạnh đáy là AE .
Vậy tỉ số diện tích của hai tam giác ABE và ADE cũng chính là tỉ số hai đường cao vẽ từ đỉnh B và D là 108/162 = 2/3 .
Xét hai tam giác ABO và ADO có cùng đáy AO và tỉ số hai đường cao tương ứng là 2/3 .
Nên diện tích tam giác ABO / diện tích tam giác ADO = 2/3 .
Ta lại xét hai tam giác ABO và ADO có hai đáy BO và DO và cùng có một đường cao đường cao tương ứng vẽ từ A .
Vậy diện tích tam giác ABO / diện tích tam giác ADO = OB / OD ( vì có cùng đường cao vẽ từ A ) .
Vậy OB / OD = 2/3 .

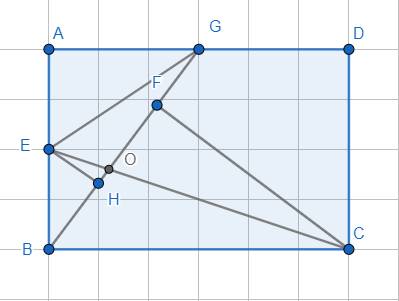
Kẻ \(EH\perp BG\), \(CF\perp BG\)
Ta có: \(S_{ABD}=S_{GBC}=\dfrac{1}{2}.AB.AD=\dfrac{1}{2}.S_{ABCD}\)
\(S_{BAG}=\dfrac{1}{2}.AB.AG=\dfrac{1}{2}.AB.\dfrac{1}{2}AD=\dfrac{1}{4}.AB.AD=\dfrac{1}{2}S_{ABD}\)
\(S_{GEB}=\dfrac{1}{2}.AG.EB=\dfrac{1}{2}.AG.\dfrac{1}{2}.AB=\dfrac{1}{4}.AG.AB=\dfrac{1}{2}S_{ABG}\)
\(\Rightarrow S_{GEB}=\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}S_{ABCD}=\dfrac{1}{8}S_{ABCD}=\dfrac{1}{4}S_{GBC}\)
\(\Leftrightarrow\dfrac{1}{2}.EH.BG=\dfrac{1}{4}.\dfrac{1}{2}CF.BG\)
\(\Leftrightarrow EH=\dfrac{1}{4}CF\)
Lại có: \(S_{OBE}=\dfrac{1}{2}OB.EH=\dfrac{1}{2}OB.\dfrac{1}{4}CF=\dfrac{1}{4}S_{OBC}\)
Ta có: \(S_{CBE}=S_{OBE}+S_{OBC}=S_{OBE}+4S_{OBE}=5S_{OBE}\)
\(S_{CBE}=5.10=50\left(cm^2\right)\)
Mà \(S_{CBE}=\dfrac{1}{2}S_{CBA}=\dfrac{1}{4}S_{ABCD}\Rightarrow S_{ABCD}=200\left(cm^2\right)\)