Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

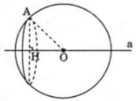
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.
Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H và bán kính HA không đổi.
Vậy các mặt cầu tâm O bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.

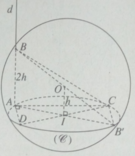
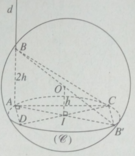
Tam giác ADC vuông tại A nên AD 2 = DC 2 - AC 2 (1)
Tam giác ABC vuông tại A nên BC 2 = AC 2 + AB 2 (2)
Từ (1) và (2) ta suy ra AD 2 + BC 2 = DC 2 + AB 2 (3)
Ta lại có:
AC 2 = DC 2 - AD 2 và BD 2 = AD 2 + AB 2 (4)
DC 2 = 4 r 2 - h 2 , AB 2 = 4 h 2 (5)
Từ (4) và (5) ta có:
AC 2 + BD 2 = DC 2 + AB 2 = 4 r 2 - h 2 + 4 h 2 = 4 r 2 (6)
Từ (3) và (6) ta có: AD 2 + BC 2 = AC 2 + BD 2 (không đổi)

Ta có AH ⊥ DC. Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông. Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng ( α ).

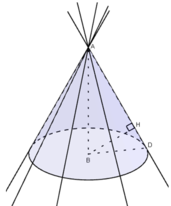
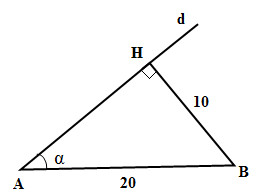
Từ B vẽ đường thẳng vuông góc với d và cắt d tại H.
Ta có BH = 10cm = d(B,d)
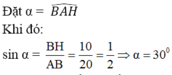
Vậy đường thẳng d nằm trên mặt nón có đỉnh là A, trục là đường thẳng AB và góc ở đỉnh là 2α = 60 °

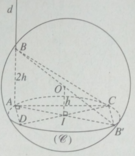
Diện tích tam giác BCD bằng:
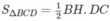
Diện tích này lớn nhất khi AI // CD.

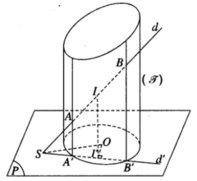
Gọi (P) là mặt phẳng đi qua S và vuông góc với trục của mặt trụ ( J ). Mặt phẳng (P) cắt ( J ) theo một đường tròn tâm O. Ta hãy xét một vị trí của đường thẳng d. Gọi A, B là giao điểm của d với ( J ) và I là trung điểm của đoạn AB. Chiếu A, B, I theo phương vuông góc với mặt phẳng (P) ta được các điểm theo thứ tự là A’ , B’ , I’ thẳng hàng với S, trong đó A’, B’ nằm trên đường tròn tâm O trong mặt phẳng (P) và I’ là trung điểm của đoạn A’B’. Do đó điểm I’ luôn luôn nằm trên đường tròn đường kính SO trong mặt phẳng (P) và đường thẳng II’ vuông góc với (P). Ta suy ra đường thẳng II’ nằm trên mặt trụ ( J ′) chứa đường tròn đường kính SO nằm trong (P) và có trục song song với trục của mặt trụ ( J ) .
Tất nhiên, điểm I chỉ nằm trong phần mặt trụ ( J ′) thuộc miền trong của mặt trụ ( J )

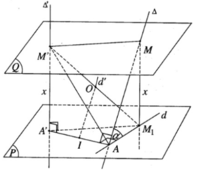
Hình tứ giác A’M’M M 1 là hình chữ nhật nên tâm O cũng là trung điểm của A’M. Do đó khi x thay đổi thì mặt phẳng (Q) thay đổi và điểm O luôn luôn thuộc đường thẳng d’ đi qua trung điểm I của đoạn AA’ và song song với đường thẳng ∆ . Vì mặt cầu tâm O luôn luôn đi qua hai điểm cố định A, A’nên nó có tâm O di động trên đường thẳng d’. Do đó mặt cầu tâm O luôn luôn chứa đường tròn tâm I cố định có đường kính AA’ cố định và nằm trong mặt phẳng cố định vuông góc với đường thẳng d’.


Xét mặt phẳng (P) qua điểm A và (P) vuông góc với đường thẳng a. GỌi giao của (P) với a là điểm I. Xét mặt cầu tâm O bán kính r = OA; mặt cầu này giao với mặt phẳng (P) theo đường tròn tâm I là hình chiếu vuông góc của O lên (P) và bán kính IA = r2 cố định