Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dễ mà bạn :)) cái này dùng qui tắc công với chèn điểm là nuột =)
a) \(\overrightarrow{PQ}+\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{NP}+\overrightarrow{PQ}+\overrightarrow{MN}\)
\(=\overrightarrow{NQ}+\overrightarrow{MN}=\overrightarrow{MN}+\overrightarrow{NQ}=\overrightarrow{MQ}\left(đpcm\right)\)
( quá chi tiết rồi nha bạn... )
b) Ta có: \(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{NQ}+\overrightarrow{QP}+\overrightarrow{MQ}+\overrightarrow{QN}\)
\(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}+\overrightarrow{NQ}+\overrightarrow{QN}\)
\(\Rightarrow\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}\left(đpcm\right)\)

Vận dụng tính chất giao hoán ta có: \[\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \]
Chọn C.

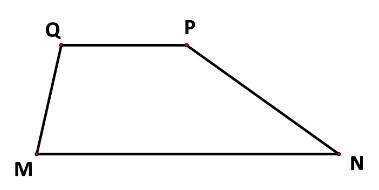
Do MQ và PN không song song với nhau nên \(\overrightarrow {MQ} \ne k\overrightarrow {NP} \). Vậy loại B và D.
Ta có: \(\overrightarrow {MN} ,\overrightarrow {PQ} \)là hai vecto ngược hướng và \(\left| {\overrightarrow {MN} } \right| = 2\left| {\overrightarrow {PQ} } \right|\)
Suy ra \(\overrightarrow {MN} = - 2\overrightarrow {PQ} \)
Vậy chọn C.

MQ là đường trung bình tam giác ABD \(\Rightarrow\overrightarrow{MQ}=\frac{1}{2}\overrightarrow{BD}\)
NP là đường trung bình tam giác CBD \(\Rightarrow\overrightarrow{NP}=\frac{1}{2}\overrightarrow{BD}\)
\(\Rightarrow\overrightarrow{NP}=\overrightarrow{MQ}\)
Câu b đề sai, \(\overrightarrow{PQ}=\overrightarrow{NM}\) mới đúng

a)
MN là đường trung bình của tam giác ABC nên \(\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{AC}\).
QP là đường trung bình của tam giác ABC nên \(\overrightarrow{QP}=\dfrac{1}{2}\overrightarrow{AC}\).
Vậy \(\overrightarrow{MN}=\overrightarrow{QP}\).
b) Giả sử:
\(\overrightarrow{MP}=\overrightarrow{MN}+\overrightarrow{MQ}\Leftrightarrow\overrightarrow{MP}-\overrightarrow{MN}-\overrightarrow{MQ}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MP}+\overrightarrow{NM}+\overrightarrow{QM}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{QM}+\overrightarrow{MP}\right)+\overrightarrow{NM}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}+\overrightarrow{NM}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}-\overrightarrow{MN}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}-\overrightarrow{QP}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{0}=\overrightarrow{0}\) ( Điều giả sử đúng).
Vậy \(\overrightarrow{MP}=\overrightarrow{MN}+\overrightarrow{MQ}.\)

Lời giải:
Xét tam giác $ABD$ có $MQ$ là đường trung bình ứng với cạnh $BD$
$\Rightarrow QM\parallel DB, \overline{MQ}=\frac{1}{2}\overline{BD}$
$\Rightarrow \overrightarrow{MQ}=\frac{1}{2}\overrightarrow{BD}(*)$
Tương tự:
$\overrightarrow{NP}=\frac{1}{2}\overrightarrow{BD}(**)$
Từ $(*); (**)\Rightarrow \overrightarrow{NP}=\overrightarrow{MQ}$
Việc cm $\overrightarrow{PQ}=\overrightarrow{NM}$ tương tự.

Do \(\overrightarrow{NP}=\overrightarrow{DC}\); \(\overrightarrow{AM}=\overrightarrow{BA}\Rightarrow\overrightarrow{MA}=\overrightarrow{AB}\).
Do tứ giác ABCD là hình bình hành nên \(\overrightarrow{AB}=\overrightarrow{DC}\).
Vì vậy \(\overrightarrow{NP}=\overrightarrow{MA}\) nên tứ giác NPAM là hình bình hành.
Vì vậy \(\overrightarrow{PA}=\overrightarrow{NM}\). (1)
Mà \(\overrightarrow{MN}=\overrightarrow{DA}\) suy ra \(\overrightarrow{NM}=\overrightarrow{AD}\) . (2)
Mặt khác \(\overrightarrow{AD}=\overrightarrow{BC}\) (do tứ giác ABCD là hình bình hành). (3)
Từ (1);(2);(3) suy ra:\(\overrightarrow{PA}=\overrightarrow{BC}\).
Mà \(\overrightarrow{PQ}=\overrightarrow{BC}\Rightarrow\overrightarrow{PQ}=\overrightarrow{PA}\).
Vì vậy hai điểm A và Q trùng nhau nên \(\overrightarrow{AQ}=\overrightarrow{0}\).



vec tơ hả ban