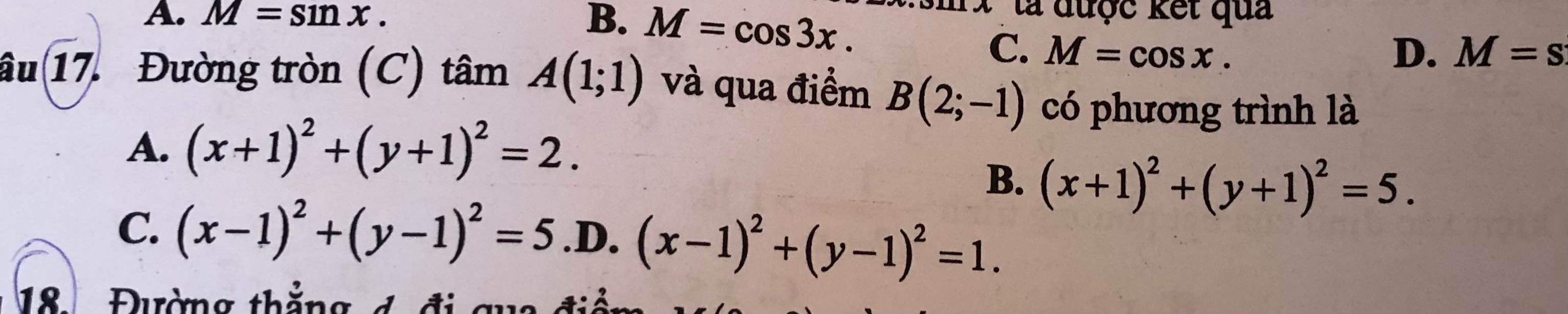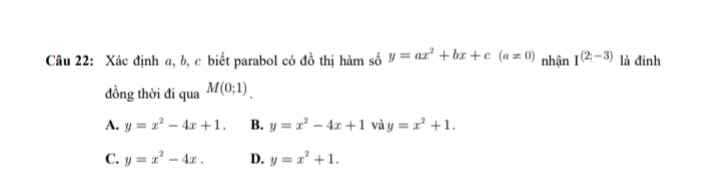Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3.
Do \(sin\left(x+k2\pi\right)=sinx\Rightarrow sin\left(x+2020\pi\right)=sinx\)
\(sin\left(\dfrac{\pi}{2}+x\right)=cos\left(\dfrac{\pi}{2}-\dfrac{\pi}{2}-x\right)=cos\left(-x\right)=cosx\)
\(A=\dfrac{sinx+sin3x+sin5x}{cosx+cos3x+cos5x}=\dfrac{sinx+sin5x+sin3x}{cosx+cos5x+cos3x}\)
\(=\dfrac{2sin3x.cosx+sin3x}{2cos3x.cosx+cos3x}=\dfrac{sin3x\left(2cosx+1\right)}{cos3x\left(2cosx+1\right)}\)
\(=\dfrac{sin3x}{cos3x}=tan3x\)
4.
a.
\(\overrightarrow{CB}=\left(2;-2\right)=2\left(1;-1\right)\)
Do đường thẳng d vuông góc BC nên nhận \(\left(1;-1\right)\) là 1 vtpt
Phương trình đường thẳng d đi qua \(A\left(-1;2\right)\) và có 1 vtpt là \(\left(1;-1\right)\) là:
\(1\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow x-y+3=0\)
b.
Gọi \(I\left(a;b\right)\) là tâm đường tròn, ta có \(\left\{{}\begin{matrix}\overrightarrow{AI}=\left(a+1;b-2\right)\\\overrightarrow{BI}=\left(a-3;b-2\right)\\\overrightarrow{CI}=\left(a-1;b-4\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AI^2=\left(a+1\right)^2+\left(b-2\right)^2\\BI^2=\left(a-3\right)^2+\left(b-2\right)^2\\CI^2=\left(a-1\right)^2+\left(b-4\right)^2\end{matrix}\right.\)
Do I là tâm đường tròn qua 3 điểm nên: \(\left\{{}\begin{matrix}AI=BI\\AI=CI\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}AI^2=BI^2\\AI^2=CI^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a+1\right)^2+\left(b-2\right)^2=\left(a-3\right)^2+\left(b-2\right)^2\\\left(a+1\right)^2+\left(b-2\right)^2=\left(a-1\right)^2+\left(b-4\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8a=8\\4a+4b=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\) \(\Rightarrow I\left(1;2\right)\)
\(\overrightarrow{AI}=\left(2;0\right)\Rightarrow R=AI=\sqrt{2^2+0^2}=2\)
Pt đường tròn có dạng:
\(\left(x-1\right)^2+\left(y-2\right)^2=4\)

7.
Phương trình đường tròn \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) với tâm \(I=\left(a;b\right)\), bán kính \(R\)
\(\Rightarrow\) Tâm đường tròn \(\left(x-1\right)^2+\left(y+2\right)^2=4\) có tọa độ \(\left(1;-2\right)\)
Kết luận: Tâm đường tròn có tọa độ \(\left(1;-2\right)\).

\(\overrightarrow{AB}=\left(1;-2\right)\Rightarrow AB=\sqrt{1^2+\left(-2\right)^2}=\sqrt{5}\)
(C) tâm A đi qua B nên có bán kính \(R=AB=\sqrt{5}\)
Phương trình:
\(\left(x-1\right)^2+\left(y-1\right)^2=5\)

18.
\(-x^2+2x-5\le0\) có \(\left\{{}\begin{matrix}a=-1< 0\\\Delta'=1-5=-4< 0\end{matrix}\right.\)
\(\Rightarrow-x^2+2x-5\le0\) ; \(\forall x\in R\)
19.
Thay tọa độ lần lượt các đáp án lên thì chỉ D đúng
20.
Chu vi đường tròn: \(2\pi R=40\pi\left(cm\right)\)
Số đo của cung: \(\dfrac{35.2\pi}{40\pi}=\dfrac{7}{4}\)

Ta có: \(x^2-6x+m-2=0\)
\(\Rightarrow\Delta=6^2-4\left(m-2\right)\)
Để phương tình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\Rightarrow36-4m+8>0\Leftrightarrow44>4m\Leftrightarrow11>m\)
Câu D


Câu 1: Cho t=1 ta có \(\left\{{}\begin{matrix}x=1+1\\y=2-2.1\\z=3+1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\\z=4\end{matrix}\right.\)
Vậy điểm M là M(2,0,4). Khoanh B.
Câu 2: Ta có tọa độ điểm O thuộc (d) là: O(1,2,3)
Để (d') cũng là phương trình tham số của (d) thì (d') phải đi qua điểm O(1,2,3)
Quan sát đáp án ta thấy đáp án B đúng.