Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì A là giao điểm của (d) với trục Oy nên x=0
=>y=-3

Tam giác AMB vuông cân tại M có trọng tâm G => GB=GA (=GD) => G là tâm ngoại tiếp tam giác BAD => ^AGD = 2^ABD = 900
a) \(AG:3x-y-13=0\Leftrightarrow\hept{\begin{cases}x=t\\y=3t-13\end{cases}}\Rightarrow G\left(t_1;3t_1-13\right),A\left(t_2;3t_2-13\right)\)
\(\overrightarrow{DG}=\left(t_1-7;3t_1-11\right)\); \(\overrightarrow{DG}\)vuông góc với VTCP (1;3) của AG
\(\Rightarrow\left(t_1-7\right)+3\left(3t_1-11\right)=0\Leftrightarrow t_1=4\Rightarrow G\left(4;-1\right)\)
\(\Rightarrow\overrightarrow{GA}=\left(t_2-4;3t_2-12\right)\)
Ta có; \(\left(t_2-4\right)^2+\left(3t_2-12\right)^2=GA^2=d^2\left(D,AG\right)=10\)
\(\Leftrightarrow\orbr{\begin{cases}t_2=5\\t_2=3\end{cases}}\Rightarrow\orbr{\begin{cases}A\left(5;2\right)\\A\left(3;-4\right)\end{cases}}\). Mà hoành độ của A nhỏ hơn A nên \(A\left(3;-4\right)\).
b) E là trung điểm BM, có \(\overrightarrow{AG}=\left(1;3\right)\Rightarrow\overrightarrow{AE}=\left(\frac{3}{2};\frac{9}{2}\right)\Rightarrow E\left(\frac{9}{2};\frac{1}{2}\right)\Rightarrow\overrightarrow{ED}=\left(\frac{5}{2};-\frac{5}{2}\right)\)
\(\Rightarrow ED:\hept{\begin{cases}x=7+m\\y=-2-m\end{cases}}\Rightarrow B\left(7+m;-2-m\right)\)
\(\Rightarrow\overrightarrow{GB}=\left(3+m;-1-m\right)\)
Lại có: \(\left(3+m\right)^2+\left(1+m\right)^2=GB^2=GA^2=10\Leftrightarrow\orbr{\begin{cases}m=0\\m=-4\end{cases}}\Rightarrow\orbr{\begin{cases}B\left(7;-2\right)\left(l\right)\\B\left(3;2\right)\end{cases}}\)
Đường thẳng AB: đi qua \(B\left(3;2\right)\),VTCP \(\overrightarrow{AB}\left(0;6\right)\)\(\Rightarrow AB:\hept{\begin{cases}x=3\\y=2+t\end{cases}}\Leftrightarrow x-3=0.\)

vẽ đồ thị:
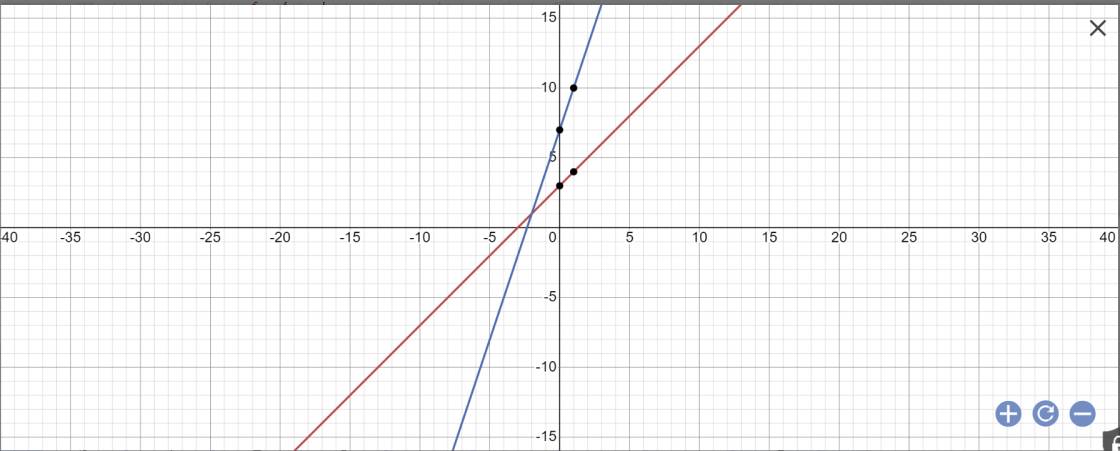
a: Phương trình hoành độ giao điểm là:
\(3x+7=x+3\)
=>3x-x=3-7
=>2x=-4
=>x=-2
Thay x=-2 vào y=x+3, ta được:
y=-2+3=1
Vậy: K(-2;1)
b: Sửa đề: I là trung điểm của đoạn thẳng nối bởi hai giao điểm của (d1) và (d2) với trục Oy
Tọa độ giao điểm của (d1) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=x+3=0+3=3\end{matrix}\right.\)
Tọa độ giao điểm của (d2) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=3x+7=3\cdot0+7=7\end{matrix}\right.\)
Tọa độ I là:
\(\left\{{}\begin{matrix}x=\dfrac{0+0}{2}=0\\y=\dfrac{3+7}{2}=\dfrac{10}{2}=5\end{matrix}\right.\)
Vậy: I(0;5)
Ta có: I(0;5); K(-2;1); O(0;0)
\(IK=\sqrt{\left(-2-0\right)^2+\left(1-5\right)^2}=\sqrt{2^2+4^2}=2\sqrt{5}\)
\(IO=\sqrt{\left(0-0\right)^2+\left(0-5\right)^2}=\sqrt{0^2+5^2}=5\)
\(KO=\sqrt{\left(0+2\right)^2+\left(0-1\right)^2}=\sqrt{2^2+1^2}=\sqrt{5}\)
Vì \(IK^2+KO^2=IO^2\)
nên ΔKIO vuông tại K
c: Vì ΔKIO vuông tại K
nên \(S_{IKO}=\dfrac{1}{2}\cdot IK\cdot KO=\dfrac{1}{2}\cdot2\sqrt{5}\cdot\sqrt{5}=5\)
Nó chỉ đúng khi A, B nằm trong cùng một mặt phẳng góc phần tư thứ nhất hoặc ba thôi.
Chẳng hạn ở hình này, dễ thấy rằng MN là đường trung bình của hình thang ABDC(AC//BD) \(\Rightarrow MN=\frac{AC+BD}{2}\)
Lại có \(MN=y_M;AC=y_A;BD=y_B\)(vì trong trường hợp này tung độ của các điểm đều dương)
\(\Rightarrow y_M=\frac{y_A+y_B}{2}\)(đpcm thứ 1)
Tương tự, ta cũng có \(x_M=\frac{x_1+x_2}{2}\)(MP là đường trung bình của hình thang ABFE)
Nếu A, B nằm trong cùng một mặt phẳng góc phần tư thứ hai hoặc bốn thì:
Nếu như này thì cũng như trường hợp trên, ta chứng minh \(x_M=\frac{x_A+x_B}{2}\)một cách dễ dàng (MP là đường trung bình của hình thang ABFE(AE//BF))
Nhưng còn về y thì nó hơi khác một chút:
Dễ thấy \(MN=\frac{AC+BD}{2}\)
Vì tất cả các tung độ trong trường hợp này đều âm nên ta có \(-y_M=\frac{-y_A-y_B}{2}\)rốt cuộc vẫn có \(y_M=\frac{y_A+y_B}{2}\)
Còn trường hợp 2 điểm A, B nằm trên 2 góc phần tư khác nhau thì mình đang nghĩ.
Ý bạn là công thức \(x_M=\frac{x_A+x_B}{2}\)và \(y_M=\frac{y_A+y_B}{2}\)nếu M là trung điểm của AB đúng không?