K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
S
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
8 tháng 5 2021
Ta có :
\(ab-c=ab-a+a-c=a\left(b-1\right)+\left(a-c\right)\)
\(\Rightarrow\left|ab-c\right|=\left|a\left(b-1\right)+\left(a-c\right)\right|\)
\(\Rightarrow\left|ab-c\right|\le\left|a\left(b-1\right)\right|+\left|a+c\right|\)
\(\Rightarrow\left|ab-c\right|\le\left|a\right|\left|b-1\right|+\left|a-c\right|\)
Mà \(\left|a\right|< 1;\left|b-1\right|< 10;\left|a-c\right|< 10\)
\(\Rightarrow\left|ab-c\right|< 1.10+10\)
\(\Rightarrow\left|ab-c\right|< 20\left(đpcm\right)\)
BT
4 tháng 7 2016
có \(\left|a\right|< 1\),\(\left|b-1\right|< 10\)suy ra \(\left|a\right|.\left|b-1\right|< 10\Rightarrow\left|a\left(b-1\right)\right|< 10\Leftrightarrow\left|ab-a\right|< 10\)
\(\Leftrightarrow-10< ab-a< 10\)(1)
có \(\left|a-c\right|< 10\Leftrightarrow-10< a-c< 10\)(2)
cộng lần lượt các vế của (1) và (2) ta có \(-10+\left(-10\right)< ab-a+a-c< 10+10\Leftrightarrow-20< ab-c< 20\)
suy ra \(\left|ab-c\right|< 20\)
làm giúp mình 2 bài này ạ
KV
29 tháng 10 2023
Lần sau chụp hình rõ hơn nhé em. Hình mờ khó nhìn hình chính xác lắm
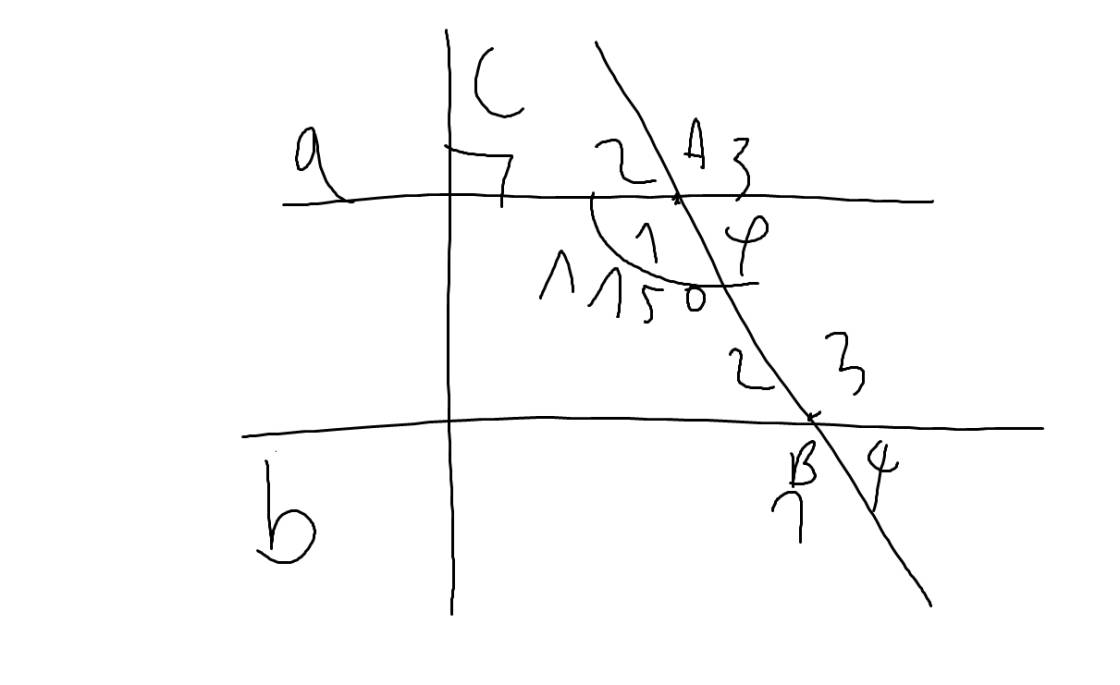
Bài 3:
a) Do c ⊥ a
a // b
⇒ c ⊥ b
b) Ta có:
∠A₃ = ∠A₁ = 115⁰ (đối đỉnh)
Do a // b
⇒ ∠B₃ = ∠A₁ = 115⁰ (so le trong)
⇒ ∠B₁ = ∠B₃ = 115⁰ (đối đỉnh)
29 tháng 10 2023
4:
a: Ot là phân giác của \(\widehat{AOB}\)
=>\(\widehat{tOB}=\widehat{tOA}=\dfrac{\widehat{AOB}}{2}=\dfrac{120^0}{2}=60^0\)
\(\widehat{tOB}=\widehat{yBO}\left(=60^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ot//By
b: \(\widehat{tOA}+\widehat{xAO}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên Ot//Ax
Ax//Ot
Ot//By
Do đó: Ax//By
3:
a: a//b
c\(\perp\)a
Do đó: c\(\perp\)b
b: a//b
=>\(\widehat{A_1}+\widehat{B_2}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{B_2}+115^0=180^0\)
=>\(\widehat{B_2}=65^0\)
a//b
=>\(\widehat{A_1}=\widehat{B_3}\)(hai góc so le trong)
mà \(\widehat{A_1}=115^0\)
nên \(\widehat{B_3}=115^0\)
\(\widehat{A_1}=\widehat{A_3}\)(hai góc đối đỉnh)
mà \(\widehat{A_1}=115^0\)
nên \(\widehat{A_3}=115^0\)
