Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Vì mặt phẳng (P) đi qua A, B nên
3 a - 2 b + 6 c - 2 = 0 b = 2 ⇔ a = 2 - 2 c b = 2 ⇒ ( P ) : ( 2 - 2 c ) x + 2 y + c z = 0
Khoảng cách từ tâm I (1;2;3) của (S) đến (P) là:
d(I,(P))= ( 2 - 2 c ) + 2 . 2 + c . 3 - 2 ( 2 - 2 c ) 2 + 2 2 + c 2 = c + 4 5 c 2 - 8 c + 8
Khi đó bán kính của đường tròn giao tuyến là:
r= 25 - ( c + 4 ) 2 5 c 2 - 8 c + 8 = 124 c 2 - 208 c + 184 5 c 2 - 8 c + 8
Để r đạt giá trị nhỏ nhất thì hàm số
f(t)= 124 t 2 - 208 t + 184 5 t 2 - 8 t + 8 trên [1;+ ∞ ) phải nhỏ nhất
Ta có: f'(t)= 48 t 2 + 144 t - 192 ( 5 t 2 - 8 t + 8 ) 2 ,
f'(t)=0
⇔
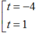
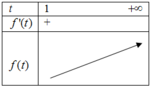
Khi đó hàm số đạt giá trị nhỏ nhất tại t=1 ⇒ c=1
Ta có: T=a+b+c=2-2c+2=4-c=3

Chọn C
* Ta có: ![]() trong đó a;b;c không đồng thời bằng 0. Mặt cầu (S) có tâm I (1;2;3) và bán kính R=5.
trong đó a;b;c không đồng thời bằng 0. Mặt cầu (S) có tâm I (1;2;3) và bán kính R=5.
Do mặt phẳng (P) chứa đường thẳng AB nên ta có:
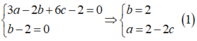
* Bán kính đường tròn giao tuyến là ![]() trong đó
trong đó
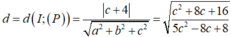
Để bán kính đường tròn nhỏ nhất điều kiện là d lớn nhất 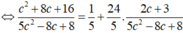 lớn nhất
lớn nhất 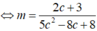 lớn nhất.
lớn nhất.
Coi hàm số ![]() là một phương trình ẩn c ta được
là một phương trình ẩn c ta được
5mc²-2 (4m+1)c+ (8m-3)=0,
phương trình có nghiệm c 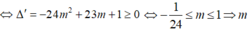 lớn nhất
lớn nhất
<=> c = 1 => a = 0 => M = 2a + b – c = 1

Đáp án B
Phương pháp:
- Đưa phương trình mặt phẳng (P) về dạng chỉ còn 1 tham số.
- (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất <=> d(I;(P)) max, trong đó: I là tâm mặt cầu (S).
Cách giải:
![]()

![]()
( S ) : x - 1 2 + y - 2 2 + z - 3 2 = 25 có tâm I(1;2;3) và bán kính R = 5
- (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất <=> d(I;(P)) max, trong đó: I là tâm mặt cầu (S)
Ta có
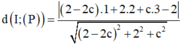
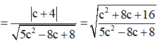
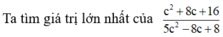
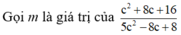
Ta có:
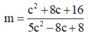
![]()
![]()
![]()
![]()
![]()
(*) có nghiệm
![]()
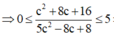
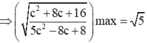
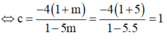
Khi đó T =a+b+c =2-2c+2+c=4-1 =3

Đáp án A
Phương pháp:
+) Để mặt phẳng (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất thì d ( I ; ( P ) ) m a x
+) Gọi H và K lần lượt là chân đường vuông góc của I trên (P) và trên đường thẳng AB. Ta có: HI ≤ IK
![]()
Cách giải:
![]()
![]()
![]()
Khi đó mặt phẳng (P) có dạng :
![]()
Mặt cầu (S) có tâm I(1;2;3), bán kính R = 5
Gọi H và K lần lượt là chân đường vuông góc của I trên (P) và trên đường thẳng AB. Ta có : HI ≤ IK
Để mặt phẳng (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất thì
![]()
![]()
=>Phương trình đường thẳng AB:
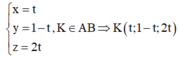
![]()
Vì
![]()
![]()
![]()
![]()
![]()
là 1 VTPT của (P)
=> I H → và vec tơ pháp tuyến n ( P ) → = ( 2 - 2 c ; 2 ; c ) cùng phương
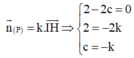
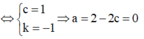
![]()

Lần sau em đăng bài ở học 24 để mọi người giúp đỡ em nhé!
Link đây: Cộng đồng học tập online | Học trực tuyến
1. Gọi I là tâm của mặt cầu cần tìm
Vì I thuộc d
=> I( a; -1; -a)
Mặt cầu tiếp xúc với hai mặt phẳng (p), (Q). nên ta co:
d(I; (P))=d(I;(Q))
<=> \(\frac{\left|a+2\left(-1\right)+2\left(-a\right)+3\right|}{\sqrt{1^2+2^2+2^2}}=\frac{\left|a+2\left(-1\right)+2\left(-a\right)+7\right|}{\sqrt{1^2+2^2+2^2}}\)
\(\Leftrightarrow\frac{\left|-a+1\right|}{3}=\frac{\left|-a+5\right|}{3}\Leftrightarrow a=3\)
=> I(3; -1; -3) ; bán kinh : R=d(I; P)=2/3
=> Phương trình mặt cầu:
\(\left(x-3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
đáp án C.
2. Gọi I là tâm mặt cầu: I(1; -1; 0)
Ta có: Phương trình mặt phẳng (P) tiếp xúc vs mặt Cầu S tại M
=> IM vuông góc vs mặt phẳng (P)
=> \(\overrightarrow{n_p}=\overrightarrow{MI}=\left(1;0;0\right)\)
=> Phương trình mặt phẳng (P) có véc tơ pháp tuyến: \(\overrightarrow{n_p}\)và qua điểm M
1(x-0)+0(y+1)+0(z-0) =0<=> x=0
đáp án B
3.
\(f\left(x\right)=\dfrac{1}{256}\left(2x+3\right)^{10}=\dfrac{1}{256} \sum \limits_{k=0} ^{10}C_{k}^{10}(2x)^k.3^{10-k}\)
Để có hệ số x^8 thì k=8 khi đó hệ số của x^8 là:
\(\dfrac{1}{256}C_{8}^{10}.2^8.3^{10-8}=405\)
đáp án D
4.
pt <=> \(\left(2.5\right)^{x^2-3}=10^{-2}.10^{3x-3}\)
\(\Leftrightarrow10^{x^2-3}=10^{3x-5}\)
\(\Leftrightarrow x^2-3=3x-5\Leftrightarrow x^2-3x+5=0\)
=> theo định lí viet tổng các nghiệm bằng 3, tích các nghiệm bằng 5
Đáp án A

đã hỏi thầy giáo và đã hiêu câu này. Quả thực đáp án A là đúng
Cảm ơn ai đang đã quan tâm đến.

\(d\left(I,\left(P\right)\right)=\frac{\left|-2.2-1.1+2.3-10\right|}{\sqrt{2^2+1^2+2^2}}=3\)
Bán kính đường tròn \(\left(C\right)\)là: \(\frac{14\pi}{2\pi}=7\)
Bán kính \(r\)của mặt cầu \(\left(S\right)\)là: \(\sqrt{3^2+7^2}=\sqrt{58}\).


Đáp án đúng : C