Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\widehat{MON}=180^0-\widehat{MAN}=120^0\)
\(S=4\pi R^2=36\pi\Rightarrow R=3\Rightarrow OM=ON=3\)
Áp dụng định lý hàm cos cho tam giác MON:
\(MN=\sqrt{OM^2+ON^2-2OM.ON.cos\widehat{MON}}=\sqrt{3^2+3^2-2.3.3.cos120^0}=3\sqrt{3}\)

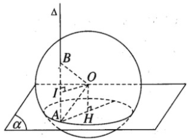
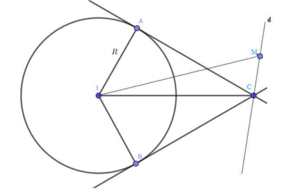
Mặt phẳng (ABO) qua tâm O của hình cầu nên cắt mặt cầu theo đường tròn lớn qua A và B. Gọi I là trung điểm của đoạn AB ta có OI ⊥ AB. Vì AB // OH nên AIOH là hình chữ nhật.
Do đó
![]()
Vậy AB = 2AI = r
Chú ý: Có thể nhận xét rằng tam giác OAB cân tại O (OA = OB) và có góc ∠ OAB = 60 ° nên OAB là tam giác đều và suy ra AB = OA = OB = r.

Chọn A
Điểm M(1;0;0) là 1 điểm thuộc (P)
Vì (P) // (Q) nên
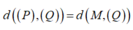
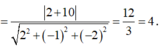
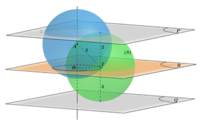
Giả sử I(a;b;c) là tâm của (S). Vì (S) tiếp xúc với cả (P) và (Q) nên bán kính mặt cầu (S) là:
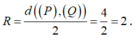
Do đó IA = 2 nên I luôn thuộc mặt cầu (T) tâm A, bán kính 2.
Ngoài ra
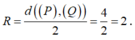
![]()
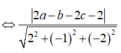
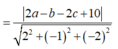
![]()
![]()
![]()
Do đó I luôn thuộc mặt phẳng (R): 2x-y-2z+4=0.
Gọi H là hình chiếu vuông góc của A lên (R). Vì A, (R) cố định nên H cố định.
Ta có
![]()
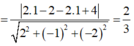
![]()
do đó tam giác AHI vuông tại H nên
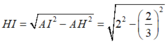
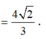
Vậy I luôn thuộc đường tròn tâm H, nằm trên mặt phẳng (R), bán kính
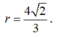

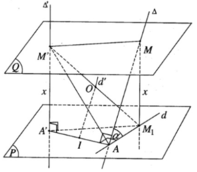
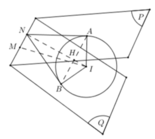
Vì mặt phẳng (P) qua A và vuông góc với Δ′ nên AA’ thuộc (P). Vì M thuộc ∆ mà d là hình chiếu vuông góc của ∆ trên (P) nên M 1 thuộc d. Vì MA ⊥ AA′ ⇒ M 1 A ⊥ AA′
Mặt khác M 1 A ⊥ M′A′ nên ta suy ra M 1 A ⊥ (AA′M′). Do đó M 1 A ⊥ M′A và điểm A thuộc mặt cầu đường kính M’ M 1
Ta có M′A′ ⊥ (P) nên M′A′ ⊥ A′ M 1 , ta suy ra điểm A’ cũng thuộc mặt cầu đường kính M’ M 1
Ta có (Q) // (P) nên ta suy ra
M M 1 ⊥ (Q) mà MM’ thuộc (Q), do đó M 1 M ⊥ MM′
Như vậy 5 điểm A, A’, M, M’, M 1 cùng thuộc mặt cầu (S) có đường kính M’ M 1 . Tâm O của mặt cầu (S) là trung điểm của đoạn M’ M 1
Ta có M ' M 1 2 = M ' A ' 2 + A ' M 1 2 = M ' A ' 2 + A ' A 2 + AM 1 2 = x 2 + a 2 + x 2 cot 2 α vì M M 1 = x
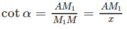
Bán kính r của mặt cầu (S) bằng (M′ M 1 )/2 nên
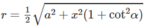

Đáp án A
Phương pháp giải:
Xét vị trí tương đối của mặt phẳng, gọi phương trình tổng quát của mặt phẳng và tính toán dựa vào điều kiện tiếp xúc
Lời giải:
Gọi phương trình mặt phẳng cần tìm là (P): ax+by+cz+d=0
![]()
suy ra mp(P)//BC hoặc đi qua trung điểm của BC.
Mà B C → = ( - 4 ; 0 ; 0 ) và mp vuông góc với mp (Oyz) => (P) //BC
Với (P) //BC => a = 0 => by+cz+d=0



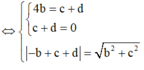

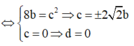
suy ra có ba mặt phẳng thỏa mãn
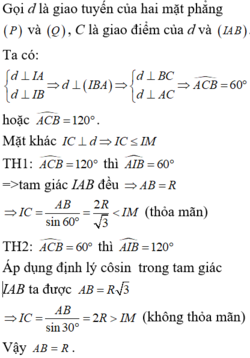


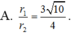
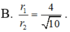
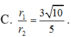
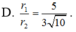
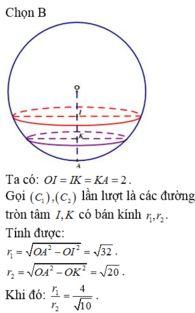
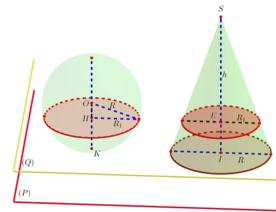
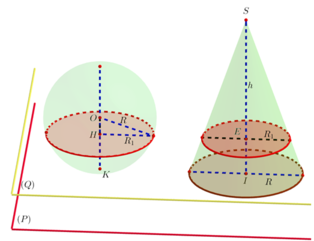


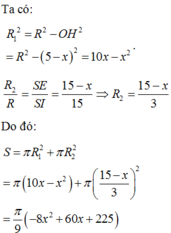
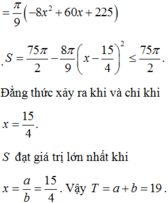
Đáp án đúng : B