Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai giá trị cho cùng công suất tiêu thụ trong mạch thõa mãn Z L 1 + Z L 2 = 2 Z C → Z C = 38 Ω .
Mặc khác
P = 25 34 P m a x ⇒ cos 2 φ = 25 34 ⇔ R 2 R 2 + Z L 1 − Z C 2 = 25 34 → R = 30 Ω.
Đáp án B

Khi L = L 1 thì dòng điện cùng pha với điện áp → hiện tượng cộng hưởng → Z C = Z L 1 = 2 π f L 1 .
Khi L = L 2 xảy ra cực đại điện áp hiệu dụng trên cuộn dây Z L 2 = R 2 + Z C 2 Z C ⇔ 2 π f L 2 = 50 2 + 2 π f L 1 2 2 π f L 1 → f = 25 Hz.
Đáp án A

Đáp án B
+ Khi f = f1 điện áp hiệu dụng trên tụ là cực đại.
P = 0,75Pmax → 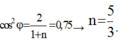 .
.
+ Khi f = f2 = f1 + 100 Hz, điện áp trên cuộn cảm là cực đại → 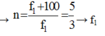 → f1 = 150 Hz
→ f1 = 150 Hz

Đáp án C
+ Khi L = L 0 công suất tiêu thụ của mạch là cực đại → mạch xảy ra cộng hưởng Z L = Z C
→ Khi đó
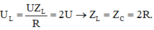
Chuẩn hóa R = 1 → Z C = 2
+ Thay đổi L để điện áp hiệu dụng trên cuộn cảm là cực đại
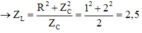
→ Công suất tiêu thụ của mạch


Chọn C.
Khi
L = L 0 ⇒ U = L 2 U ⇔ U . Z L R = 2 U ⇔ Z L = 2 R ⇔ Z C = 2 R ⇒ cos φ 0 = 1
Khi
L = L max ⇒ Z L max = R 2 + Z C 2 Z C = 2 , 5 R ⇒ cos φ 1 = 2 5 5
cos φ 1 2 cos φ 0 2 = P 1 P 0 ⇔ P 1 = 160 W .

Đáp án A
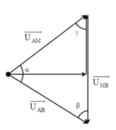
+ Biểu diễn vecto các điện áp.
+ Áp dụng định lý sin trong tam giác, ta có:
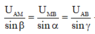
![]()
luôn không đổi
Biến đổi lượng giác

![]()
Khi đó
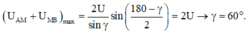
Các vecto hợp với nhau thành tam giác đều => khi xảy ra cực đại u chậm pha hơn i một góc
30
0
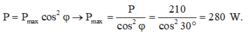 .
.

Đáp án B
f thay đổi,
f
1
,
U
C
m
a
x
max,
f
2
,
U
L
max nên ta có công thức 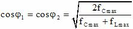 (1)
(1)
Mặt khác: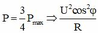
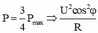 .
.
Thay vào (1), dễ dàng
tìm được f 1 = 150 Hz.

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$
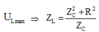
Giá trị của L để công suất tiêu thụ trên mạch là cực đại L = 0 , 5 ( L 1 + L 2 ) = 0 , 45 H .
Đáp án D