Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

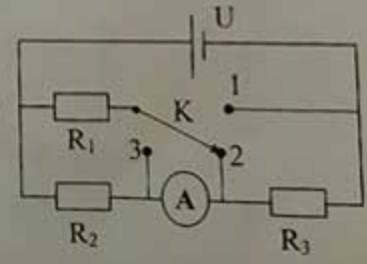
TH1: khoá K ở vị trí 1
\(R_{tđ}=\dfrac{R_1\left(R_2+R_3\right)}{R_1+R_2+R_3}\left(\text{Ω}\right)\)
\(I=\dfrac{U}{R_{tđ}}=\dfrac{U\left(R_1+R_2+R_3\right)}{R_1\left(R_2+R_3\right)}\left(A\right)\)
\(I_{A1}=\dfrac{R_1}{R_1+R_2+R_3}.I=\dfrac{R_1}{R_1+R_2+R_3}.\dfrac{U\left(R_1+R_2+R_3\right)}{R_1\left(R_2+R_3\right)}=\dfrac{U}{R_2+R_3}\left(A\right)\)
Các trường hợp còn lại làm tương tự, ta có
TH2: vị trí khoá K ở 2
\(I_{A2}=\dfrac{UR_1}{R_1R_2+R_2R_3+R_3R_1}\left(A\right)\)
TH3: vị trí khoá K ở 3
\(I_{A3}=\dfrac{U\left(R_1+R_2\right)}{R_1R_2+R_2R_3+R_3R_1}\left(A\right)\)
Ta thấy \(I_{A3}>I_{A2}\left(R_1+R_2>R_1\right)\)
Xét \(I_{A2}-I_{A1}=\dfrac{UR_1}{R_1R_2+R_2R_3+R_3R_1}-\dfrac{U}{R_2+R_3}=\dfrac{-UR_2R_3}{\left(R_2+R_3\right)\left(R_1R_2+R_2R_3+R_3R_1\right)}< 0\Rightarrow I_{A2}< I_{A1}\)
Xét \(I_{A3}-I_{A1}=\dfrac{U\left(R_1+R_2\right)}{R_1R_2+R_2R_3+R_3R_1}-\dfrac{U}{R_2+R_3}=\dfrac{UR_2^2}{\left(R_2+R_3\right)\left(R_1R_2+R_2R_3+R_3R_1\right)}>0\Rightarrow I_{A3}>I_{A1}\)
\(\Rightarrow I_{A3}>I_{A1}>I_{A2}\Rightarrow\left\{{}\begin{matrix}I_{A3}=11mA\\I_{A1}=9mA\\I_{A2}=6mA\end{matrix}\right.\)
b,xét \(\dfrac{I_{A3}}{I_{A2}}=\dfrac{R_1+R_2}{R_1}=\dfrac{11}{6}\Leftrightarrow5R_1=6R_2\Leftrightarrow R_2=\dfrac{5}{6}.2019=\dfrac{2265}{2}\left(\text{Ω}\right)\)
Xét \(\dfrac{I_{A1}}{I_{A2}}=\dfrac{R_1R_2+R_2R_3+R_3R_1}{R_1R_2+R_3R_1}=\dfrac{9}{6}\Rightarrow R_3=\dfrac{R_1R_2}{2R_2-R_1}=\dfrac{10095}{4}\left(\text{Ω}\right)\)

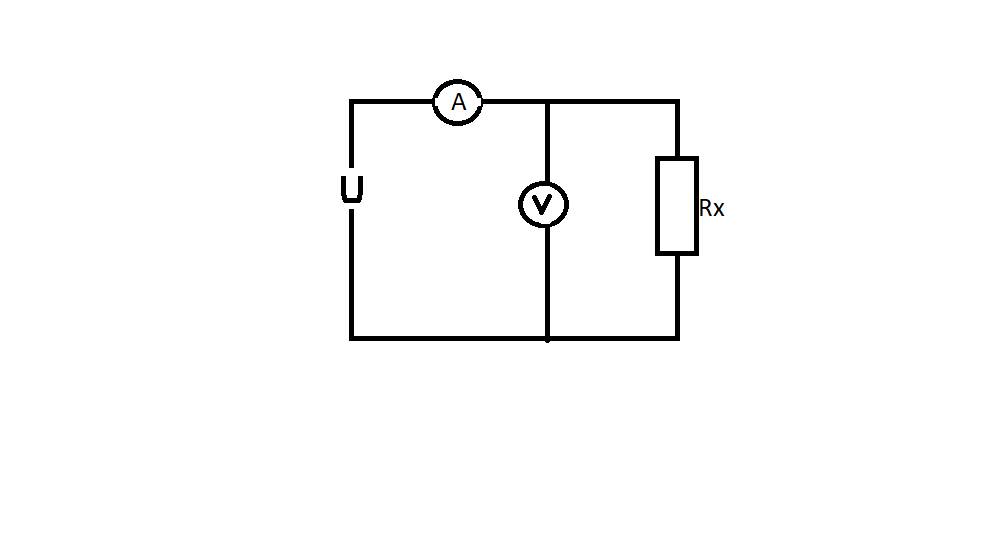
Ban đầu chưa hoán đổi: \(R_X//R_V\)
\(\Rightarrow U=U_V=U_X=3V\)
\(I_A=I_m=12mA=0,012A\)
\(\Rightarrow R_{tđ}=\dfrac{R_X\cdot R_V}{R_X+R_V}=\dfrac{U}{I}=\dfrac{3}{0,012}=250\) \(\left(1\right)\)
Khi hoán đổi mạch mới là: \(R_VntR_X\)
\(\Rightarrow R_{tđ}=R_X+R_V=\dfrac{U}{I}=\dfrac{3}{0,004}=750\Omega\)
Như vậy: \(\left(1\right)\Rightarrow R_X\cdot R_V=187500\)
Áp dụng công thức: \(R^2-S\cdot R+P=0\) với \(\left\{{}\begin{matrix}S=R_X+R_V\\P=R_X\cdot R_V\end{matrix}\right.\)
Khi đó: \(R^2-750R+187500=0\)

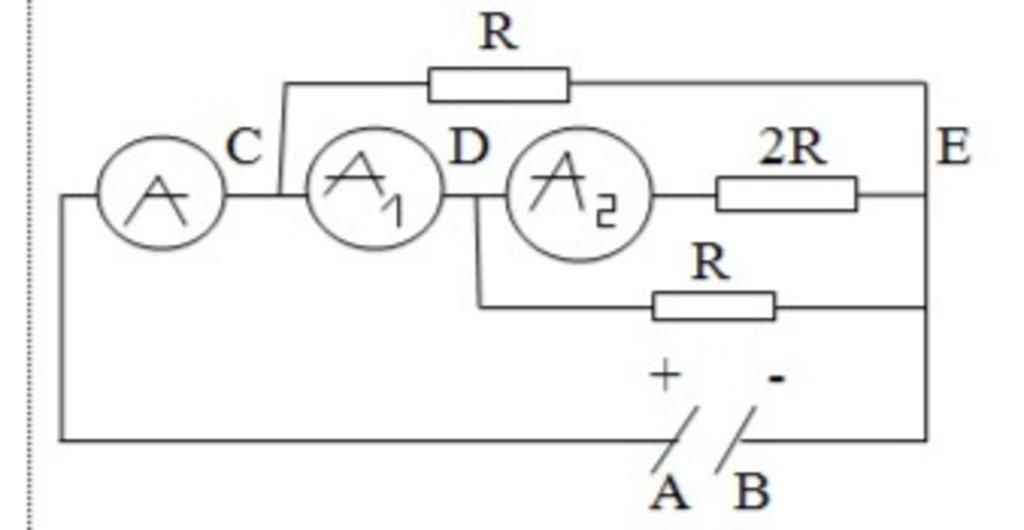
a) Tính số chỉ \(\dfrac{R}{R_A}\):
I\(_R\) = I\(_{A1}\) - I\(_{A2}\) = 1 - 0,4 = 0,6 (A)
U\(_R\) = 0,6
Ta có: U\(_{DE}\) = ( R\(_A\) + 2R ) . 0,4
Mà: U\(_{DE}\) = U\(_R\)
\(\Leftrightarrow\) 0,6R = ( R\(_A\) + 2R ) . 0,4 \(\Leftrightarrow\) \(\dfrac{R}{R_A}\) = -2
b) hình như đề bài cho A\(_1\)= 1A rồi mà bạn

a, ta có I1+I2=I=3(A)
\(I_1=\dfrac{36}{30}=1,2\left(A\right)\)
\(\Rightarrow I_2=3-I_1=1,8\left(A\right)\)
b, \(R_2=\dfrac{U}{I_2}=\dfrac{36}{1,8}=20\left(\Omega\right)\)
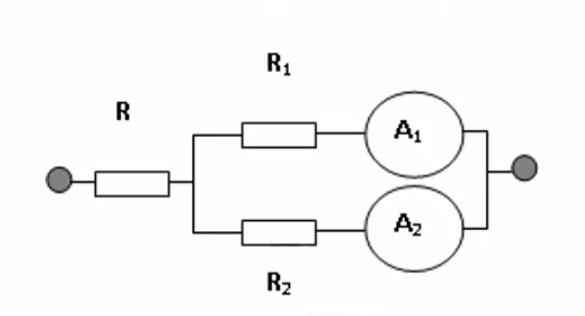
\(a,=>R1//R2\)
\(=>Ia=I1+I2=3A\)
\(=>Uv=U1=U2=36V\)
\(=>I1=\dfrac{U1}{R1}=\dfrac{36}{30}=1,2A=Ia1\)
\(=>I2=I1-I1=3-1,2=1,8A=Ia2\)
b, \(=>Rtd=\dfrac{30R2}{30+R2}=\dfrac{U}{Ia}=\dfrac{36}{3}=12=>R2=20\left(om\right)\)

R nt (R1 // R2)
a,\(=>U1=U2=Ia1.R1=20.1,5=30V\)
\(=>30=Ia2.R2=>R2=30\left(ôm\right)\)
\(=>Rtd=R+\dfrac{R1R2}{R1+R2}=22\left(ôm\right)\)
b.\(=>U=\left(Ia1+Ia2\right).Rtd=\left(1+1,5\right).22=55V\)

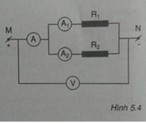
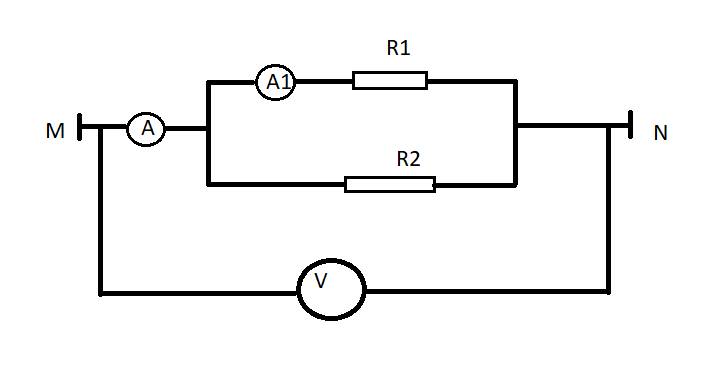
Vì R 1 mắc song song R 2 nên U 1 = U 2 = U V = U M N = 36V
Số chỉ của ampe kế 1 là: 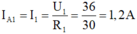
Số chỉ của ampe kế 2 là: 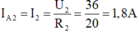

\(a,12V=V_1+V_2\)
\(\rightarrow V_1=4V\)
\(R_1=\dfrac{U}{I_1}=\dfrac{4}{0,8}=5\left(\Omega\right)\)
\(R_2=\dfrac{U}{I_2}=\dfrac{8}{0,8}=10\left(\Omega\right)\)
\(b,I=\dfrac{30V}{R_1+R_2}=\dfrac{30}{15}=2\left(A\right)\)
\(V=5\Omega.2A+10\Omega2A=10V+20V=30V\)
\(A=I=2\left(A\right)\)

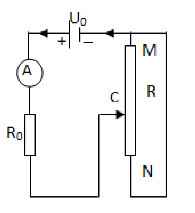
vẽ lại mạch ta đc R0nt(RMC//RNC)
RMC+RNC=R
đặt RMC=x \(R_{CNM}=\dfrac{x.\left(R-x\right)}{R}\)
\(\Rightarrow I=\dfrac{U_0}{R_0+R_{CNM}}=\dfrac{U_0}{R_0+\dfrac{x.\left(R-x\right)}{R}}\)
khi I max=2A\(\Rightarrow R_0=\dfrac{U_0}{I_{max}}=\dfrac{12}{2}=6\left(\Omega\right)\)
muốn ampe kế có gt min => RCNMmax
\(\Rightarrow R_{CNM}=\dfrac{-x^2+xR}{R}=\dfrac{-x^2+xR-\dfrac{R^2}{4}+\dfrac{R^2}{4}}{R}\)
\(R_{CNM}=\dfrac{\dfrac{R^2}{4}-\left(x-\dfrac{R}{2}\right)^2}{R}\le\dfrac{R}{4}\)
vậy \(R_{CNMmax}=\dfrac{R}{4}\) \(\Leftrightarrow x=\dfrac{R}{2}\) vậy C ở giữa R
lúc này \(I_{min}=1=\dfrac{U_0}{R_0+\dfrac{R}{4}}\Rightarrow R=24\left(\Omega\right)\)