HA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 4 2021
ĐKXĐ: ...
\(\Leftrightarrow m^2+m\left(x^2-3x-4\right)-m\sqrt{x+7}-\left(x^2-3x-4\right)\sqrt{x+7}=0\)
\(\Leftrightarrow m\left(x^2-3x-4+m\right)-\sqrt{x+7}\left(x^2-3x-4+m\right)=0\)
\(\Leftrightarrow\left(m-\sqrt{x+7}\right)\left(x^2-3x-4+m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=\sqrt{x+7}\left(1\right)\\m=-x^2+3x+4\left(2\right)\end{matrix}\right.\)
Với \(m\) nguyên tố \(\Rightarrow\) (1) luôn có đúng 1 nghiệm
Để pt có số nghiệm nhiều nhất \(\Rightarrow\) (2) có 2 nghiệm pb
\(\Rightarrow y=m\) cắt \(y=-x^2+3x+4\) tại 2 điểm pb thỏa mãn \(x\ge-7\)
\(\Rightarrow-66\le m\le\dfrac{25}{4}\Rightarrow m=\left\{2;3;5\right\}\)
CM
15 tháng 11 2017
Chọn A.
Lập bảng tần số- tần suất:
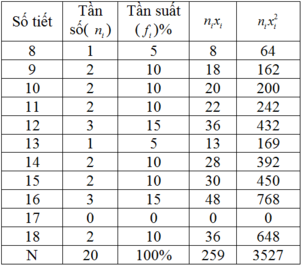
Phương sai của dãy số liệu trên là:
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 7 2021
\(\Leftrightarrow\) Với mọi \(x>0\) ta luôn có:
\(x^3-x^2-2x+m\left(x+1\right)\ge0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-2x\right)+m\left(x+1\right)\ge0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-2x+m\right)\ge0\)
\(\Leftrightarrow x^2-2x+m\ge0\) (do \(x+1>0\) ; \(\forall x>0\))
\(\Leftrightarrow m\ge-x^2+2x\)
\(\Leftrightarrow m\ge\max\limits_{x>0}\left(-x^2+2x\right)=1\)
\(\Rightarrow m=\left\{1;2;3;4;...;10\right\}\)
7 tháng 2 2020
Để pt có 2 nghiệm phân biệt và là hai số đối nhau:
\(\Leftrightarrow\hept{\begin{cases}m^4-2m^2+1-m^2-m+2>0\\m\ne-2\\x_1+x_2=0\end{cases}}\)
- \(\orbr{\begin{cases}m< 1\\m>1,546818277\end{cases}}\)
- \(m\ne-2\)
- \(\frac{2m^2-2}{m+2}=0\Rightarrow\orbr{\begin{cases}m=1\left(ktm\right)\\m=-1\left(tm\right)\end{cases}}\)
Vậy ...............
Không có số chính phương nào vì trong các thừa số của M đều có 7 xuất hiện duy nhất một lần.
Ví dụ: 7! = 1.2.3.4.5.6.7 thì thừa số 7 chỉ xuất hiện một lần nên 7! không là số chính phương.
tương tự như vậy cho các thừa số của M.