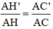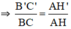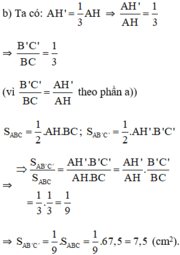Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tứ giác ADBC có
AD//BC
AC//BD
=>ADBC là hbh
=>AD=BC và BD=AC
Xét tứ giác ABCE có
AE//BC
AB//CE
=>ABCE là hbh
=>AB=CE và AE=BC
Xét tứ giác ABFC có
AB//FC
AC//BF
=>ABFC là hbh
=>AB=CF và AC=BF
=>DE=2BC và DF=2AC và EF=2BA
=>ΔABC đồng dạng với ΔFED
=>S ABC/S FED=(AB/FE)^2=1/4

gọi giao điểm của AD và EB là O mà ABDE là hình bình hành nên O là trung điểm EB
Nối BF ; CE ta đc BCEF là hình bình hành nên EB và CF cắt nhau tại trung điểm EB là O

Gọi H là giao điểm của ED và BC
=> SABHE=\(\dfrac{\left(AB+EH\right).BH}{2}=\dfrac{\left(3+6\right).4}{2}=18\left(cm^2\right)\)
Shình vuông DHC= \(\dfrac{DH.CH}{2}=\dfrac{2.1}{2}=1\left(cm^2\right)\)
Áp dụng định lí Py -ta go trong tam giác vuông EKA
EA=\(\sqrt{EK^2+KA^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
Trong tam giác vuông FEA có FE=FA => \(EF^2=\dfrac{25}{2}\)
=> SFEA=(FE.FA)/2=\(\dfrac{25}{2}:2=\dfrac{25}{4}\left(cm^2\right)\)
vậy S lục giác đã cho = SABHE+ SFEA- Shình vuông DHC=18+\(\dfrac{25}{4}-1=\dfrac{93}{4}\left(cm^2\right)\)
Nhớ tick nha ,đánh quẹo cả tay,em cảm ơn trước ak

a: Xét tứ giác ABDE có
AB//DE
AE//BD
=>ABDE là hbh
=>AB=DE=5cm và BD=AE=12cm
EC=5+15=20cm
EC^2=AE^2+AC^2
=>ΔAEC vuông tại A
b: Kẻ AH vuông góc EC tại H
=>AH=15*20/25=300/25=12cm
S ABCD=1/2*AH*(AB+CD)
=1/2*12*(5+15)=20*6=120cm2

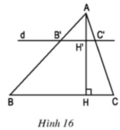
a) Theo hệ quả định lý Ta let ta có:
ΔABC có B’C’ // BC (B’ ∈ AB; C’ ∈ AC) ⇒ 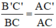
ΔAHC có H’C’ // HC (H’ ∈ AH, C’ ∈ AC) ⇒