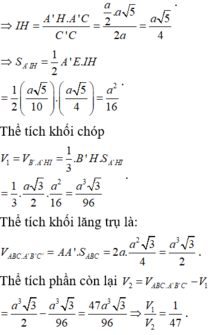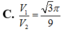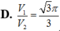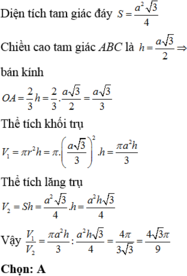Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
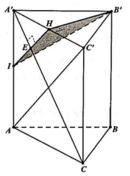
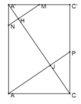
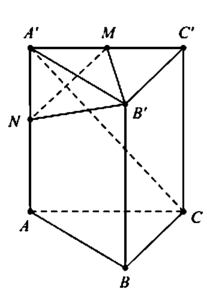Gọi M là trung điểm A’C’. Ta có
B
'
M
⊥
A
C
C
'
A
'
⇒
B
'
M
⊥
A
'
C
.
Suy ra M ∈ m p P . Kẻ M N ⊥ A ' C ( N ∈ A A ' ) ⇒ N ∈ m p P
Thiết diện cắt bởi mặt phẳng (P) và lăng trụ là tan giác B’MN
Hai tam giac A’C’C và NA’M đồng dạng ⇒ A ' N = 1 2 A ' M = a 4
Thể tích tứ diện A'B'MN là V 1 = 1 3 A ' N . S ∆ A ' B ' M = a 3 3 96
Thể tích lăng trụ là V = A A ' . S ∆ A B C = a 3 3 2 . Vậy V 1 V 2 = 1 47 .
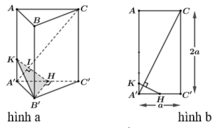
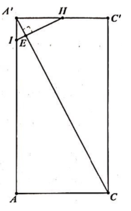
Gọi H là trung điểm của A'C', suy ra 
Trong mặt phẳng (ACC'A') kẻ 
Do đó thiết diện tạo bởi mặt phẳng (P) và khối lăng trụ là tam giác HKB'
Ta có 
và tính được 
Do đó 
Chọn D.
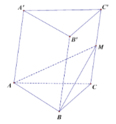
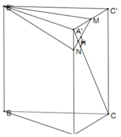
Hình chóp MABC có cùng diện tích đáy với hình lăng trụ
Và có chiều cao bằng 2 lăng trụ nên
V 2 = 1 6 V ABC . A ' B ' C ' ⇒ V 1 = 5 6 V ABC . A ' B ' C ' ⇒ V 1 V 2 = 5
Đáp án cần chọn là C
Đáp án D.
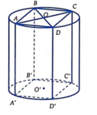
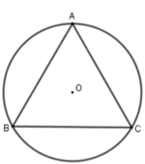
Mặt phẳng (P) cắt đường tròn đáy theo dây cung có độ dài bằng 2 r 2 − r 2 2 2 = r 2 .
Độ dài r 2 chính là độ dài cạnh của hình vuông nội tiếp đường tròn bán kính r.
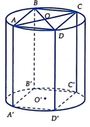
Xét hình hộp chữ nhật có đáy là hình vuông nội tiếp hình trụ. Khi đó khối hộp chữ nhật đó chia khối trụ thành 5 phần gồm một phần là khối hộp và bốn phần bằng nhau ở ngoài khối hộp nhưng ở trong khối trụ.
Thể tích khối trụ là V = π r 2 h . Thể tích khối hộp chữ nhật nói trên là V 0 = r 2 2 h = 2 r 2 h .
Suy ra V 2 = 1 4 V − V 0 = π − 2 4 r 2 h và V 1 = V − V 2 = 3 π + 2 4 r 2 h .
Do đó V 1 V 2 = 3 π + 2 π − 2 .