Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Chiết suất của lăng kính đối với tia tím và đỏ tính theo (1) là:
\(n_t=1,7311\text{≈}\sqrt{3};\)\(n_đ=1,4142\text{≈}\sqrt{2}\)
Khi góc lệch của tia tím là cực tiểu thì: \(\iota'_1=\iota_2\Rightarrow r_1=r_2=\frac{A}{2}\)
và \(D_{min}=2\iota_1-A\) hay \(\iota_1=\frac{D_{tmin}+A}{2}\)
áp dụng công thức : \(\sin\iota_1=n\sin r_1\) ta được \(\sin D_{tmin}+A_2=n_t\sin\frac{A}{2}\)
Đối với tia tím \(n_t=\sqrt{3}\) và biết \(A=60^0\), ta được:
\(\sin D_{tmin}+A_2=60^0\Rightarrow D_{tmin}=60^0\)
Góc tới của tia sáng trắng ở mặt AB phải bằng:\(i_t=60^0\)
b/ Tương tự như vậy, muốn cho góc lệch của tia đỏ là cực tiểu thì:
\(\sin\frac{D_{dmin}+A}{2}=n_d\sin\frac{A}{2}\Rightarrow D_{dmin}=30^0\)
và góc tới của tia sáng trắng trên mặt AB là: \(i_đ=45^0\)
Như vậy phải giảm góc tới trên mặt AB một góc là :\(i_t-t_đ=15^0\), tức là phải quay lăng kính quanh cạnh A một góc \(15^0\) ngược chiều kim đồng hồ.
c/Gọi \(r_{0đ}\)và \(r_{0t}\) là các góc giới hạn phản xạ toàn phần của tia đỏ và tia tím ta có:
\(\sin r_{0đ}=\frac{1}{n_d}=\frac{1}{\sqrt{2}}\Rightarrow r_{0đ}=45^0\)
\(\sin r_{0t}=\frac{1}{n_t}=\frac{1}{\sqrt{3}}\)=>r0t < r0đ .Do đó muốn cho không có tia sáng nào ló ra khỏi mặt AC của lăng kính thì phải có: r2 \(\ge\)r0đ \(\Rightarrow r_2\ge15^0\)
Hay \(\sin r_1\ge\sin\left(60^0-45^0\right)=0,2588\)
Biết \(\sin r_{1t}=\frac{\sin\iota}{n_t},\sin r_{1đ}=\frac{\sin\iota}{n_d}\); vì \(n_t\le n_đ\)nên suy ra \(r_{1t}\le\sin r_{1đ}\)(2)
Từ (1) và (2) ta thấy bất đẳng thức (1) được thõa mãn đối với mọi tia sáng, nghĩa là không có tia nào trong chùm sáng trắng ló ra khỏi mặt AC, nếu
\(\sin r_{1đ}\le0,2588\)hay \(\frac{\sin\iota}{n_đ}<0,2588\)
\(\Rightarrow\sin i\le0,2588.n_đ\)\(\Rightarrow\sin\le0,36\) .Suy ra góc tới:\(i\le21^06'\)

Đáp án A
Khoảng cách giữa 2 vân sáng liên tiếp quan sát được trên màn là:
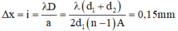

⇒ δ = i 2 t − i 2 d = 13 , 3 °
Chọn C
Tia đỏ : sin i 1 = n d sin r 1 d ⇒ sin 55 ° = 1, 6383 sin r 1 d ⇒ i 1 d = 30 ° r 1 d + r 2 d = A = 65 ° ⇒ r 2 d = 35 ° sin i 2 d = n d sin r 2 d ⇒ sin i 2 d = 1, 6383 sin 35 ° ⇒ i 2 d = 70 °
Tia tím: sin i 1 = n t sin r 1 t ⇒ sin 55 ° = 1, 6896 sin r 1 t ⇒ i 1 t = 29 ° r 1 t + r 2 t = A = 65 ° ⇒ r 2 t = 36 ° sin i 2 t = n t sin r 2 t ⇒ sin i 2 t = 1, 6896 sin 36 ° ⇒ i 2 t = 83 , 3 °
⇒ δ = i 2 t − i 2 d = 13 , 3 °

Chọn D
sin i 1 = sin D min + A 2 = n sin A 2 ⇒ sin i 1 = 1 , 635 sin 40 ° 2 ⇒ i 1 = 34 °

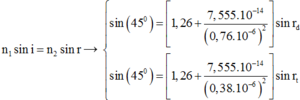
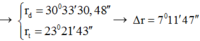
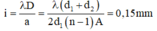
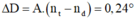
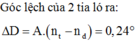
- Mỗi tia qua lăng kính bị lệch D = A(n – 1) nên góc tạo bởi hai tia ló là