Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
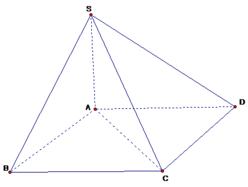
Mặt phẳng (SAC) chia khối chóp S.ABCD thành 2 khối tứ diện là : SABC,SACD

Chọn A.
Gọi O là giao điểm của AC và BD.
Mặt phẳng (SAC) và( SBD) chia khối chóp S.ABCD thành mấy khối chóp thành 4 khối chóp là các khối chóp sau S.ABO, S.ADO, S.CDO, S.BCO

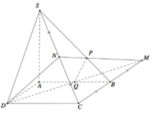
D A B C N M I G H
\(d\left(M,BN\right)=\frac{\left|13\left(-1\right)-10.2+13\right|}{\sqrt{13^2+10^2}}=\frac{20}{\sqrt{269}}\)
\(H\in\Delta\Leftrightarrow H\left(3a;2a\right)\)
Gọi I là tâm ABCD, G là giao điểm của AC và BN. Ta thấy G là trọng tâm của tam giác BCD
Suy ra \(CG=\frac{2}{3}.CI=\frac{1}{3}AC\) mà \(AM=\frac{1}{4}AC\Rightarrow MG=\frac{5}{12}AC\Rightarrow CG=\frac{4}{5}MG\)
\(\Rightarrow d\left(C,BN\right)=\frac{4}{5}d\left(M,BN\right)=\frac{16}{\sqrt{269}}\Rightarrow d\left(H,BN\right)=2d\left(C,BN\right)=\frac{32}{\sqrt{269}}\)
\(\Leftrightarrow\frac{\left|13.3a-10.2a+13\right|}{\sqrt{269}}=\frac{32}{\sqrt{269}}\Leftrightarrow a=1\) hoặc \(a=\frac{-45}{19}\)
Vì H và M nằm khác phía đối với đường thẳng BN nên \(H\left(3;2\right)\)
Tiếp.........
Ta thấy \(CM=\frac{3AC}{4}=\frac{2AB}{4}=\frac{2CD}{4}=\frac{CD}{2}=CD=CH\Rightarrow\Delta MHN\) vuông tại M
HM có phương trình \(y-2=0\Rightarrow MN:x+1=0\Rightarrow N\left(-1;0\right)\Rightarrow C\left(1;1\right),D\left(-3;-1\right)\)
Do \(\overrightarrow{CM}=3\overrightarrow{MA}\Rightarrow A\left(\frac{-5}{3};\frac{7}{3}\right)\Rightarrow I\left(\frac{-1}{3};\frac{5}{3}\right)\Rightarrow B\left(\frac{7}{3};\frac{13}{3}\right)\)
Vậy \(A\left(\frac{-5}{3};\frac{7}{3}\right);B\left(\frac{7}{3};\frac{13}{3}\right);C\left(1;1\right);D\left(-3.-1\right)\)

Có 5 mặt phẳng cách đều 5 điểm S, A, B, C, D:
Mặt phẳng đi qua 4 trung điểm của 4 cạnh bên: có 1 mặt.
Mặt phẳng đi qua tâm O và song song với từng mặt bên : có 4 mặt như vậy

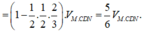
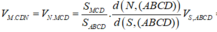
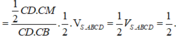
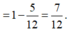
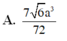
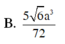
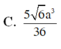
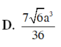


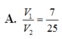
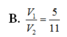
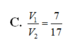
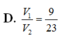


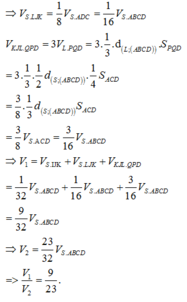
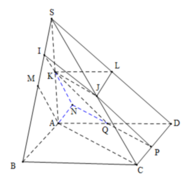
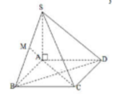
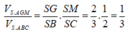
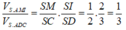
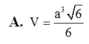
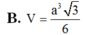
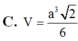
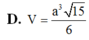
Chọn A.
Mặt phẳng (SAC) chia khối chóp S.ABCD thành 2 khối tứ diện là S.ABC và S.ACD.