Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

AB = BC = CD = DA (gt)
AE = BK = CP = DQ (gt)
Suy ra: EB = KC = PD = QA
- Xét ∆ AEQ và ∆ BKE :
AE = BK (gt)
ˆ
A
=
ˆ
B
=
90
0
A^=B^=900
QA = EB (chứng minh trên)
Do đó: ∆ AEQ = ∆ BKE (c.g.c) ⇒ EK = EQ (1)
- Xét ∆ BKE và ∆ CPK :
BK = CP (gt)
ˆ
B
=
ˆ
C
=
90
0
B^=C^=900
EB = KC (chứng minh trên)
Do đó: ∆ BKE = ∆ CPK (c.g.c) ⇒ EK = KP (2)
Xét ∆ CPK và ∆ DQP :
CP = DQ (gt)
ˆ
C
=
ˆ
D
=
90
0
C^=D^=900
DP = CK (chứng minh trên)
Do đó: ∆ CPK = ∆ DQP (c.g.c) ⇒ KP = PQ (3)
Từ (1), (2) và (3) suy ra: EK = KP = PQ = EQ
Tứ giác EKPQ là hình thoi.

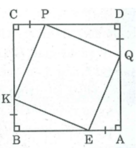
Ta có: AB = BC = CD = DA (gt)
AE = BK = CP = DQ (gt)
Suy ra: EB = KC = PD = QA
* Xét ΔAEQ và ΔBKE,ta có:
AE = BK (gt)
∠ (EAQ) = ∠ (KBE) = 90 0
QA = EB (chứng minh trên)
Suy ra: △ AEQ = △ BKE (c.g.c) ⇒ EQ = EK (1)
* Xét △ BKEvà △ CPK,ta có: BK = CP (gt)
∠ (KBE) = ∠ (PCK) = 90 0
EB = KC ( chứng minh trên)
Suy ra: △ BKE = △ CPK (c.g.c) ⇒ EK = KP (2)
* Xét △ CPK và △ DQP,ta có: CP = DQ (gt)
∠ C = ∠ D = 90 0
DP = CK ( chứng minh trên)
Suy ra: △ CPK = △ DQP (c.g.c) ⇒ KP = PQ (3)
Từ (1), (2) và (3) suy ra: EK = KP = PQ = EQ
Hay tứ giác EKPQ là hình thoi.
Mặt khác: △ AEQ = △ BKE
⇒ ∠ (AQE) = ∠ (BEK)
Mà ∠ (AQE) + ∠ (AEQ) = 90 0
⇒ ∠ (BEK) + ∠ (AEQ) = 90 0
Ta có: ∠ (BEK) + ∠ (QEK) + ∠ (AEQ ) = 180 0
Suy ra: ∠ (QEK ) = 180 0 -( ∠ (BEK ) + ∠ (AEQ) )= 180 0 - 90 0 = 90 0
Vậy tứ giác EKPQ là hình vuông.

1: AM+MB=AB
BN+NC=BC
CP+PD=CD
QD+QA=AD
mà AB=BC=CD=AD và AM=BN=CP=QD
nên BM=CN=PD=QA
2: Xét ΔMAQ vuông tại A và ΔNBM vuông tại B có
MA=NB
AQ=BM
Do đó: ΔMAQ=ΔNBM
=>MQ=MN(1)
Xét ΔMBN vuông tại B và ΔNCP vuông tại C có
MB=NC
BN=CP
Do đó: ΔMBN=ΔNCP
=>MN=NP(2)
Xét ΔNCP vuông tại C và ΔPDQ vuông tại D có
NC=PD
CP=DQ
Do đó: ΔNCP=ΔPDQ
=>NP=PQ(3)
Từ (1),(2),(3) suy ra MQ=MN=NP=PQ
ΔMAQ=ΔNBM
=>\(\widehat{AMQ}=\widehat{BNM}\)
mà \(\widehat{BNM}+\widehat{BMN}=90^0\)(ΔBMN vuông tại B)
nên \(\widehat{AMQ}+\widehat{BMN}=90^0\)
\(\widehat{AMQ}+\widehat{QMN}+\widehat{NMB}=180^0\)
=>\(90^0+\widehat{QMN}=180^0\)
=>\(\widehat{QMN}=90^0\)
Xét tứ giác MNPQ có
MN=NP=PQ=MQ
nên MNPQ là hình thoi
Hình thoi MNPQ có \(\widehat{QMN}=90^0\)
nên MNPQ là hình vuông

Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình
=>EH//BD và EH=BD/2(1)
Xét ΔBCD có
F là trung điểm của BC
G là trung điểm của CD
Do đó: FG là đường trung bình
=>FG//BD và FG=BD/2(2)
Từ (1) và (2) suy ra EH//FG và EH=FG
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của BC
Do đó: EF là đường trung bình
=>EF//AC
mà AC⊥BD
nên EF⊥BD
mà BD//EH
nên EF⊥EH
Xét tứ giác EHGF có
EH//FG
EH=FG
Do đó: EHGF là hình bình hành
mà EH⊥EF
nên EHGF là hình chữ nhật

Bạn tra gu gồ được mà,hỏi làm gì cho mệt chớ,tìm được cách làm trên gu gồ là áp dụng vào bài thôi
noi A vs C ,BvsC
ap dung tinh chat duong trug binh cua tam giac
AM=EN
MN=FE
MNEF la hinh thoi

Tự vẽ hình :)
t/g ABC có :
AE = EB
BF = FC
\(\Rightarrow\)EF - đường trung bình của tam giác ABC
\(\Rightarrow\)\(EF\)// \(AC\)\(,\)\(EF=\frac{AC}{2}\left(1\right)\)
t/g ADC có :
AH = HD
CG = GD
\(\Rightarrow\)HG - đường trung bình của tam giác ADC
\(\Rightarrow\)\(HG\)// \(AC\)\(,\)\(HG=\frac{AC}{2}\)\(\left(2\right)\)
Từ ( 1 ) và ( 2 ) \(\Leftrightarrow\)EF // HG , EF = HG
Vì tứ giác EFGH có 2 cạnh đối song song và bằng nhau
\(\Rightarrow\)EFGH - hình bình hành ( đpcm )

Dễ mà.
4 tam giác vuông bằng nhau ( c- g-c)
=> 4 cạnh huyền = nhau
+ Mặt khác Trong 1 tam giác vuông có 2 góc nhọn phụ nhau
=> EKPQ có 1 góc vuông
KL: Hình vuông
marian đề đúng đấy