Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(DF=\sqrt{25^2-15^2}=20\)
\(\sin E=\frac{DF}{EF}=\frac{20}{25}=\frac{4}{5}\) \(\Rightarrow\cos F=\frac{4}{5}\)
\(\cos E=\frac{DE}{EF}=\frac{15}{25}=\frac{3}{5}\Rightarrow\sin F=\frac{3}{5}\)
\(\tan E=\frac{DF}{DE}=\frac{20}{15}=\frac{4}{3}\Rightarrow\cot F=\frac{4}{3}\)
\(\cot E=\frac{DE}{DF}=\frac{15}{20}=\frac{3}{4}\Rightarrow\tan F=\frac{3}{4}\)
2.
\(\cos B=\frac{AB}{BC}=\frac{AB}{8}\Leftrightarrow\frac{AB}{8}\approx0,866\Rightarrow AB\approx6,928cm\)
\(AC=\sqrt{8^2-6,928^2}\approx4\)
3.
\(A=\sin10^o+\sin40^o-\cos50^o-\cos80^o=sin10^o+sin40^o-sin40^o-sin10^o=0\)
\(B=tan18^o-cot72^o+3\cdot\frac{tan21^o}{cot69^o}=tan18^o-tan18^o+3\cdot\frac{tan21^o}{tan21^o}=3\)

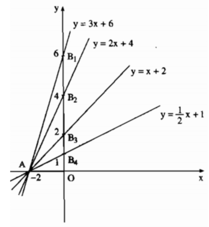
Gọi ∠ ( B 1 Ax) = α 1 ; ∠ ( B 2 Ax) = α 2 ; ∠ ( B 3 Ax) = α 3 ; ∠ ( B 4 Ax) = α 4 . Dùng máy tính bỏ túi CASIO fx – 220 tính tg α 1 , tg α 2 , tg α 3 , tg α 4 và suy ra các góc tương ứng.
Ta có:
tg α 1 = 3 ⇒ α 1 ≈ 71 ° 33 ' 54 , 18 ' '
tg α 2 = 2 ⇒ α 2 ≈ 63 ° 26 ' 5 , 82 ' '
tg α 3 = 1 ⇒ α 3 ≈ 45 °
tg α 4 = 1/2 ⇒ α 4 ≈ 26 ° 33 ' 54 , 18 ' '

Ta có:
sin²a + cos²a = 1
⇒ sin²a = 1 - cos²a
= 1 - (3/4)²
= 1 - 9/16
= 7/16
⇒ sina = √7/4
⇒ tana = sina/cosa = (√7/4)/(3/4) = √7/3

a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
b: Xét ΔABD có
AH vừa là đường cao, vừa là trung tuyến
=>ΔABD cân tại A
=>tan ADH=tan ABD=tan ABC=AC/AB=4/3
Xét ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC=HD*HC

1:
a: Xét ΔABC vuông tại A có \(tanACB=\dfrac{AB}{AC}=\dfrac{1}{\sqrt{3}}\)
=>\(\widehat{ACB}=30^0\)
b: Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}\)
=>\(\dfrac{AB}{8}=sin30=\dfrac{1}{2}\)
=>\(AB=4\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=8^2-4^2=48\)
=>\(AC=4\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH\cdot8=4\cdot4\sqrt{3}=16\sqrt{3}\\BH=\dfrac{AB^2}{BC}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH=\dfrac{16\sqrt{3}}{8}=2\sqrt{3}\left(cm\right)\\BH=\dfrac{4^2}{8}=2\left(cm\right)\end{matrix}\right.\)
c: \(cosC-tanB+cotB\)
\(=cos30-tan60+cot60\)
\(=\dfrac{\sqrt{3}}{2}-\sqrt{3}+\dfrac{\sqrt{3}}{3}=\dfrac{5}{6}\sqrt{3}-\sqrt{3}=-\dfrac{1}{6}\sqrt{3}\)