Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì \(\left\{{}\begin{matrix}AD=AB\\AI=DK\left(\dfrac{1}{2}AD=\dfrac{1}{2}DC\right)\\\widehat{BAD}=\widehat{ADK}=90^0\end{matrix}\right.\) nên \(\Delta AIB=\Delta DKA\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABI}=\widehat{DAI}\\ \Rightarrow\widehat{DAI}+\widehat{AIB}=\widehat{ABI}+\widehat{AIB}=90^0\\ \Rightarrow BI\perp AK\)

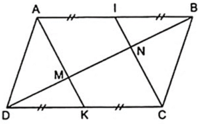
Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
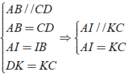
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.

a: Xét hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: EF//AB//CD
Xét ΔADC có
E là trung điểm của AD
EK//DC
Do đó: K là trung điểm của AC
hay KA=KC
Xét ΔBDC có
F là trung điểm của BC
FI//DC
Do đó: I là trung điểm của BD
hay IB=ID
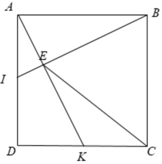
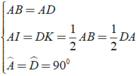

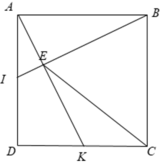

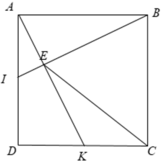

Xét Δ BAI và Δ ADK có:
⇒ Δ BAI = Δ ADK ( c - g - c )