Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

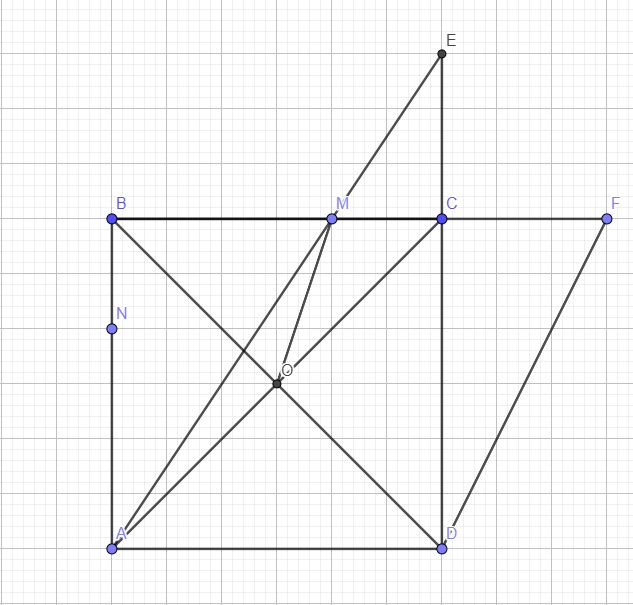
Đặt cạnh hình vuông là a, ta có \(BD=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow BO=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\Rightarrow BO.BD=a^2\)
Xét 2 tam giác vuông AED và MAB có:
\(\left\{{}\begin{matrix}\widehat{ADE}=\widehat{MBA}=90^0\\\widehat{AED}=\widehat{MAB}\left(slt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AED\sim\Delta MAB\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{BM}=\dfrac{ED}{AB}\Rightarrow BM.ED=AD.AB=a^2\)
\(\Rightarrow BM.ED=BO.BD\)
Mà \(ED=BF\) (do \(BC=CD\) và \(CE=CF\))
\(\Rightarrow BM.BF=BO.BD\Rightarrow\dfrac{BM}{BD}=\dfrac{BO}{BF}\)
Xét hai tam giác BOM và BFD có:
\(\left\{{}\begin{matrix}\dfrac{BM}{BD}=\dfrac{BO}{BF}\\\widehat{OBM}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BOM\sim\Delta BFD\left(c.g.c\right)\)

a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
=>ΔADE cân tại A
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB=góc KAC
=>ΔAHB=ΔAKC
=>AH=AK
Xét ΔADE có AH/AD=AK/AE
nên HK//DE
c:
góc HBD+góc D=90 độ
góc KCE+góc E=90 độ
mà góc D=góc E
nên góc HBD=góc KCE
góc MBC=góc HBD
góc MCB=góc KCE
mà góc HBD=góc KCE
nên góc MBC=góc MCB
=>ΔMBC cân tại M

a, ABCD là hình vuông (gt)
=> AD = DC (đn)
xét tg ADE và tg CDF có : AE = CF (Gt)
^EAD = ^DCF = 90 do ..
=> tg ADE = tg CDF (2cgv)
=> DE = DF (1) và
^AED = ^DFC (đn) ; AB//CD do ABCD là hv (gt) => ^AED = ^EDC (slt)
=> EDC = ^DFC
có ^DFC + ^FDC = 90 do ...
=> ^EDC + ^FDC = 90
=> ^EDF = 90 và (1)
=> tg EDF vuông cân tại D (Đn)
b, tg BEF vuông tại B ; I là trung điểm của EF (gt) => BI = EF/2 (đl)
tgEDF vuông tại D (câu a); I là trung điểm của EF (gt) => DI = EF/2 (Đl)
=> BI = DI
=> I thuộc đường trung trực của BD (Đl)
có O;C thuộc đường trung trực của BD (dễ tự cm)
=> O;C;I thẳng hàng
khong lam được hjnh hoi mjnh nha


a, Xét \(\Delta ADE\)và \(\Delta DCF\)ta có :
\(DC=AD\)(theo tính chất của hinh vuông )
\(AE=CF\left(gt\right)\)
\(\widehat{DAE}=\widehat{DCF}=90^0\)
\(\Rightarrow\Delta ADE=\Delta DCF\left(c.g.c\right)\)
\(\Rightarrow\hept{\begin{cases}DE=DF\\\widehat{ADE}=\widehat{CDF}\end{cases}}\)
Mà \(\widehat{ADE}=\widehat{EDC}=90^0\)(tính chất hình vuông )
Nên \(\widehat{CDF}=\widehat{EDC}=90^0\)
Xét \(\Delta EDF\)ta có :
\(\widehat{EDF}=90^0\)
\(\Rightarrow\Delta EDF\)vuông tại D
Mà \(DE=DF\left(cmt\right)\)
Nên \(\Delta DEF\)là tam giác vuông cân tại D
b, Xét \(\Delta BEF\)vuông tại B , ta có :
BI là đường trung tuyến ( I là trung điểm EF )
\(\Rightarrow BI=\frac{1}{2}EF\)
Xét \(\Delta DFE\)vuông tại D , ta có :
DI là đường trung tuyến ( I là trung điểm EF )
\(\Rightarrow DI=\frac{1}{2}EF\)
Mà \(BI=\frac{1}{2}EF\left(cmt\right)\)
Nên DI=BI
Có DI=BI
\(\Rightarrow I\)là đường trung trực của BD (1)
Có DC=CB (tính chất hình vuông ABCD )
\(\Rightarrow C\)thuộc đường trung trực của BD (2)
Có O là trung điểm BD ( tính chất hình vuông ABCD )
\(\Rightarrow O\)thuộc đường trung trực BD (3)
Từ 1 , 2 , 3
\(\Rightarrow O,C,I\)thẳng hàng
Chúc bạn học tốt !

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

a) Xét ΔCAH vuông tại H và ΔCDH vuông tại H có
CH chung
AH=DH(gt)
Do đó: ΔCAH=ΔCDH(hai cạnh tương ứng)
Suy ra: CA=CD(Hai cạnh tương ứng)
Xét ΔCAD có CA=CD(cmt)
nên ΔCAD cân tại C(Định nghĩa tam giác cân)
b) Xét ΔBAH vuông tại H và ΔBDH vuông tại H có
BH chung
AH=DH(gt)
Do đó: ΔBAH=ΔBDH(hai cạnh góc vuông)
Suy ra: BA=BD(Hai cạnh tương ứng)
Xét ΔABC và ΔDBC có
CA=CD(cmt)
BC chung
AB=DB(cmt)
Do đó: ΔABC=ΔDBC(c-c-c)
Suy ra: \(\widehat{BAC}=\widehat{BDC}\)(hai góc tương ứng)
mà \(\widehat{BAC}=90^0\)(gt)
nên \(\widehat{BDC}=90^0\)
hay KD\(\perp\)CE(đpcm)
c) Xét ΔCAE vuông tại A và ΔCDK vuông tại D có
CA=CD(cmt)
\(\widehat{ACE}=\widehat{DCK}\)(hai góc đối đỉnh)
Do đó: ΔCAE=ΔCDK(cạnh góc vuông-góc nhọn kề)
Suy ra: CE=CK(hai cạnh tương ứng)
Xét ΔCEK có CE=CK(cmt)
nên ΔCEK cân tại C(Định nghĩa tam giác cân)
d) Ta có: ΔCAE=ΔCDK(cmt)
nên AE=DK(hai cạnh tương ứng)
Ta có: BA+AE=BE(A nằm giữa B và E)
BD+DK=BK(D nằm giữa B và K)
mà BA=BD(cmt)
và AE=DK(cmt)
nên BE=BK
Ta có: CE=CK(cmt)
nên C nằm trên đường trung trực của EK(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: BE=BK(cmt)
nên B nằm trên đường trung trực của EK(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BC là đường trung trực của EK
hay BC\(\perp\)EK
mà BC\(\perp\)AD(cmt)
nên AD//EK(Định lí 1 từ vuông góc tới song song)