Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, 700 góc nào bạn ?
b, Vì AB là tiếp tuyến (O) => ^ABO = 900
AO giao BC = K
AB = AC ; OB = OC = R
Vậy OA là đường trung trực đoạn BC
Xét tam giác ABO vuông tại B, đường cao BK
Áp dụng định lí Pytago tam giác ABO vuông tại B
\(AB=\sqrt{AO^2-BO^2}=\sqrt{16-4}=2\sqrt{3}\)cm
Áp dụng hệ thức : \(BK.AO=BO.AB\Rightarrow BK=\frac{BO.AB}{AO}=\frac{4\sqrt{3}}{4}=\sqrt{3}\)cm
Vì AO là đường trung trực => \(BC=2KB=2\sqrt{3}\)cm
Chu vi tam giác ABC là :
\(P_{ABC}=AB+AC+BC=2AB+BC=4\sqrt{3}+2\sqrt{3}=6\sqrt{3}\)cm

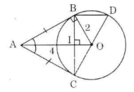
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét ΔCBD có :
CI = IB
CO = OD (bán kính)
⇒ BD // HO (HO là đường trung bình của BCD) ⇒ BD // AO.
c) Theo định lí Pitago trong tam giác vuông OAC:
A C 2 = O A 2 – O C 2 = 4 2 – 2 2 = 12
=> AC = √12 = 2√3 (cm)
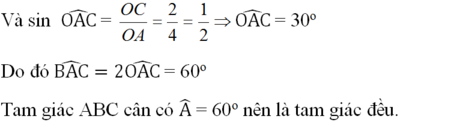
Do đó AB = BC = AC = 2√3 (cm).

a: Xét (O) có
AD là đường kính
AB\(\perp\)AD tại A
Do đó: AB là tiếp tuyến của (O)
Xét tứ giác AOMB có \(\widehat{OAB}+\widehat{OMB}=90^0+90^0=180^0\)
nên AOMB là tứ giác nội tiếp
=>A,O,M,B cùng thuộc một đường tròn
b: Xét (O) có
OD là bán kính
DK\(\perp\)DO tại D
Do đó: DK là tiếp tuyến của (O)
Xét (O) có
BA,BM là các tiếp tuyến
Do đó: OB là phân giác của góc AOM
=>\(\widehat{AOM}=2\cdot\widehat{MOB}\)
Xét (O) có
KM,KD là các tiếp tuyến
Do đó: OK là phân giác của góc DOM
=>\(\widehat{DOM}=2\cdot\widehat{KOM}\)
Ta có: \(\widehat{MOA}+\widehat{MOD}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{KOM}+\widehat{BOM}\right)=180^0\)
=>\(2\cdot\widehat{KOB}=180^0\)
=>\(\widehat{KOB}=90^0\)
=>OK\(\perp\)OB
Xét (O) có
BA,BM là các tiếp tuyến
Do đó: BA=BM
Xét (O) có
KD,KM là các tiếp tuyến
Do đó: KD=KM
Xét ΔOBK vuông tại O có OM là đường cao
nên \(BM\cdot MK=OM^2\)
=>\(BM\cdot MK=\left(\dfrac{1}{2}AD\right)^2=\dfrac{1}{4}AD^2=\dfrac{1}{4}AB^2\)
c: Ta có: BA=BM
=>B nằm trên đường trung trực của AM(1)
Ta có: OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra BO là đường trung trực của AM
=>BO\(\perp\)AM
mà BO\(\perp\)OK
nên AM//OK
Xét ΔDEA có
O là trung điểm của AD
OK//AE
Do đó: K là trung điểm của DE

a: Xét (O) có
AD là đường kính
AB\(\perp\)AD tại A
Do đó: AB là tiếp tuyến của (O)
Xét tứ giác AOMB có \(\widehat{OAB}+\widehat{OMB}=90^0+90^0=180^0\)
nên AOMB là tứ giác nội tiếp
=>A,O,M,B cùng thuộc một đường tròn
b: Xét (O) có
OD là bán kính
DK\(\perp\)DO tại D
Do đó: DK là tiếp tuyến của (O)
Xét (O) có
BA,BM là các tiếp tuyến
Do đó: OB là phân giác của góc AOM
=>\(\widehat{AOM}=2\cdot\widehat{MOB}\)
Xét (O) có
KM,KD là các tiếp tuyến
Do đó: OK là phân giác của góc DOM
=>\(\widehat{DOM}=2\cdot\widehat{KOM}\)
Ta có: \(\widehat{MOA}+\widehat{MOD}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{KOM}+\widehat{BOM}\right)=180^0\)
=>\(2\cdot\widehat{KOB}=180^0\)
=>\(\widehat{KOB}=90^0\)
=>OK\(\perp\)OB
Xét (O) có
BA,BM là các tiếp tuyến
Do đó: BA=BM
Xét (O) có
KD,KM là các tiếp tuyến
Do đó: KD=KM
Xét ΔOBK vuông tại O có OM là đường cao
nên \(BM\cdot MK=OM^2\)
=>\(BM\cdot MK=\left(\dfrac{1}{2}AD\right)^2=\dfrac{1}{4}AD^2=\dfrac{1}{4}AB^2\)
c: Ta có: BA=BM
=>B nằm trên đường trung trực của AM(1)
Ta có: OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra BO là đường trung trực của AM
=>BO\(\perp\)AM
mà BO\(\perp\)OK
nên AM//OK
Xét ΔDEA có
O là trung điểm của AD
OK//AE
Do đó: K là trung điểm của DE

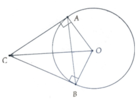
a, ∆OAC = ∆OBC (c.g.c)
=> O B C ^ - O A B ^ = 90 0
=> đpcm
b, Sử dụng hệ thức lượng trong tam giác vuông OBC tính được OC=25cm

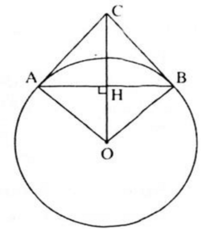
a) Gọi H là giao điểm của OC và AB, ΔAOB cân tại O (OA = OB, bán kính). OH là đường cao nên cũng là đường phân giác. Do đó:
![]()

Suy ra: CB vuông góc với OB, mà OB là bán kính của đường tròn (O)
⇒ CB là tiếp tuến của đường tròn (O) tại B. (điều phải chứng minh)
b) Ta có: OH vuông góc AB nên H là trung điểm của AB (quan hệ vuông góc giữa đường kính và dây)

Vậy OC = 25 cm
Kẻ đường kính BF thì F, A, D thẳng hàng. Gọi DE là tiếp tuyến kẻ từ D. Khi đó ta có: D E 2 = D A . D F => AF = 6cm. Từ đó tính được OB = 10 cm