OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tập huấn miễn phí ra đề kiểm tra và chấm phiếu trắc nghiệm dành cho giáo viên khối THCS

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
NN
Nguyễn Ngọc Tấn Tài
27 tháng 12 2018 - olm

Cho hình vuông ABCD cạnh a. Trên các cạnh BC và CD lấy 2 điểm M, N sao cho góc MAN=45 độ. Trên tia đối của tia DC lấy điểm E sao cho DE=BM

a)cm AE=AM rồi từ đó suy ra AN vuông góc EM

b) tìm vị trí M thuộc BC và N thuộc CD sao cho diện tích tam giác AMN lớn nhất
#Toán lớp 8
0
T
TrịnhAnhKiệt
1 tháng 10 2023

Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, trên tia đối của tia DC lấy điểm N sao cho BM=DN.
a, CMR tam giác ABM=ADN
b,CMR tam giác AMN vuông cân
c,Tia phân giác của góc MAN cắt CD tại P. CMR MP=BM+DP
d,Gọi AP cắt MN tại I. CMR MP=BM+DP
#Toán lớp 8
1
NL
Nguyễn Lê Phước Thịnh
24 tháng 11 2023

a: Xét ΔABM vuông tại B và ΔADN vuông tại D có

AB=AD

BM=DN

Do đó: ΔABM=ΔADN

b: ΔABM=ΔADN

=>AM=AN và \(\widehat{MAB}=\widehat{NAD}\)

\(\widehat{MAB}+\widehat{DAM}=\widehat{BAD}=90^0\)

mà \(\widehat{MAB}=\widehat{NAD}\)

nên \(\widehat{DAM}+\widehat{DAN}=90^0\)

=>\(\widehat{MAN}=90^0\)

Xét ΔAMN có AM=AN và \(\widehat{MAN}=90^0\)

nênΔAMN vuông cân tại A

d: ΔAMN cân tại A

mà AI là đường phân giác

nên I là trung điểm của MN và AI\(\perp\)MN tại I

=>AP\(\perp\)MN tại I

Xét ΔPNM có

PI là đường cao

PI là đường trung tuyến

Do đó: ΔPNM cân tại P

=>PN=PM

=>PM=PD+DN=PD+BM

Đúng(0)
BT
bạch thục quyên
30 tháng 3 2018 - olm
cho hình vuông ABCD có cạnh bằng a. các điểm M,N nằm trên các cạnh BC, CD ( M khác B,M khác C,N khác C,N khác D) sao cho góc MAN=45 độ. gọi E,F lần lượt là giao điểm của AM, AN trên BDa) chứng minh chu vi tam giác MNC=2ab) chứng minh rằng MF vuông góc với ANC) tính diện tích tam giác AMN khi M,N lần lượt là giao điểm của tia phân giác của góc BAC với cạnh BC; tia phân giác của góc DAC với cạnh CD và...
Đọc tiếp

cho hình vuông ABCD có cạnh bằng a. các điểm M,N nằm trên các cạnh BC, CD ( M khác B,M khác C,N khác C,N khác D) sao cho góc MAN=45 độ. gọi E,F lần lượt là giao điểm của AM, AN trên BD

a) chứng minh chu vi tam giác MNC=2a

b) chứng minh rằng MF vuông góc với AN

C) tính diện tích tam giác AMN khi M,N lần lượt là giao điểm của tia phân giác của góc BAC với cạnh BC; tia phân giác của góc DAC với cạnh CD và a=4cm
#Toán lớp 8
0
NN
Như Nguyễn
13 tháng 9 2015 - olm
Bài 1: Cho tam giác ABC .Trên tia AC lấy điểm M sao cho AM = AB. Trên tia AB lấy điểm N sao cho AN = AC. Chứng minh tứ giác BMCN là hình thangBài 2: Cho tam giác ABC vuông tại A. Lấy điểm M thuộc cạnh BC sao cho AM= 1/2 BC, N là trung điểm cạnh AB. Chứng minh:a) Tam giác ABC cân ---- b) Tứ giác MNAC là hình thang vuông Bài 3: Cho hình thang cân ABCD ( AB // CD ) ---- a) Chứng minh góc ACD = góc BCD ---- b) Gọi E là giao điểm của...
Đọc tiếp

Bài 1: Cho tam giác ABC .Trên tia AC lấy điểm M sao cho AM = AB. Trên tia AB lấy điểm N sao cho AN = AC. Chứng minh tứ giác BMCN là hình thang

Bài 2: Cho tam giác ABC vuông tại A. Lấy điểm M thuộc cạnh BC sao cho AM= 1/2 BC, N là trung điểm cạnh AB. Chứng minh:

a) Tam giác ABC cân ---- b) Tứ giác MNAC là hình thang vuông 

Bài 3: Cho hình thang cân ABCD ( AB // CD ) ---- a) Chứng minh góc ACD = góc BCD ---- b) Gọi E là giao điểm của AC và BD. C/minh EA = EB

Bài 4: Cho ABCD là hình thang ( AB // CD, AB < CD ). Kẻ các đường cao AE,BF của hình thang. C/minh rằng DE = CF 

Bài 5: Cho ABCD là hình thang ( AB // CD ) có DB là đường phân giác góc D và AE là đường phân giác góc A ( E thuộc DC ). Biết AE // BC và O là giao điểm của AE với DB. CMR:

a) AE vuông góc với DB

b) AD // BE và AD = BE

c) E là trung điểm của DC 

d) Xác định dạng của tứ giác BCEO

e) Biết góc BEC = 80 độ. Hãy tính các góc của hình thang ABCD 
#Toán lớp 8
1
NL
Nguyễn Lê Phước Thịnh
5 tháng 10 2022

Bài 4:

Xét ΔAED vuông tại E và ΔBFC vuông tại F có

AD=BC

góc D=góc C

Do đó: ΔAED=ΔBFC

=>DE=CF
Bài 3:

a: Xét ΔADC và ΔBCD có

AD=BC

AC=BD

DC chung

Do đó: ΔADC=ΔBCD

=>góc ACD=góc BDC

b: Ta co: góc ACD=góc BDC

=>góc EAB=góc EBA
=>ΔEAB cân tại E

Đúng(0)
2D
22 - Đỗ Nhật Minh - 6A17
24 tháng 10 2023 - olm

Bài 1. Cho hình vuông ABCD có cạnh bằng a. Trên cạnh BC lấy điểm M, trên tia đối của tia DC lấy điểm N sao cho BM = DN. a) Chứng minh tam giác AMN là tam giác vuông cân. b) Gọi E là trung điểm của MN. Tia AE cắt CD tại F. Chứng minh tam giác FAN = tam giác FAM.
#Toán lớp 8
1
KV
Kiều Vũ Linh
24 tháng 10 2023

 

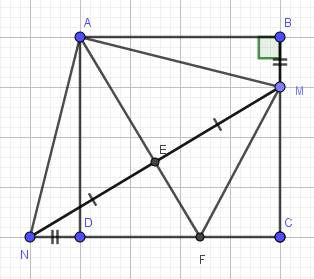
a) Do ABCD là hình vuông (gt)

\(\Rightarrow AB=AD\)

\(\widehat{ABM}=\widehat{ADN}=90^0\)

Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ADN\) có:

\(AB=AD\left(cmt\right)\)

\(BM=DN\left(gt\right)\)

\(\Rightarrow\Delta ABM=\Delta ADN\) (hai cạnh góc vuông)

\(\Rightarrow AM=AN\) (hai cạnh tương ứng)

\(\widehat{BAM}=\widehat{DAN}\) (hai góc tương ứng)

Ta có:

\(\widehat{BAM}+\widehat{DAM}=90^0\)

\(\Rightarrow\widehat{DAN}+\widehat{DAM}=90^0\)

\(\Rightarrow\widehat{MAN}=90^0\)

\(\Delta AMN\) có:

\(AM=AN\left(cmt\right)\)

\(\Rightarrow\Delta AMN\) cân tại A

Mà \(\widehat{MAN}=90^0\left(cmt\right)\)

\(\Rightarrow\Delta AMN\) vuông cân tại A

b) Do \(\Delta AMN\) cân tại A

E là trung điểm của MN

\(\Rightarrow AE\) là đường trung tuyến, cũng là đường cao của \(\Delta AMN\)

\(\Rightarrow AE\perp MN\)

\(\Rightarrow EF\perp MN\)

Xét hai tam giác vuông: \(\Delta FEM\) và \(\Delta FEN\) có:

\(EM=EN\left(gt\right)\)

\(EF\) là cạnh chung

\(\Rightarrow\Delta FEM=\Delta FEN\) (hai cạnh góc vuông)

\(\Rightarrow FM=FN\) (hai cạnh tương ứng)

Xét \(\Delta FAN\) và \(\Delta FAM\) có:

\(FA\) là cạnh chung

\(FN=FM\left(cmt\right)\)

\(AN=AM\left(cmt\right)\)

\(\Rightarrow\Delta FAN=\Delta FAM\left(c-c-c\right)\)

Đúng(3)
TH
tran huy vu
7 tháng 8 2019 - olm

Cho hình vuông ABCD cạnh 6cm. Trên cạnh BC, CD lấy hai điểm M,N  sao cho góc MAN= 45 độ. Trên tia đối của tia DC lấy điểm K sao cho DK=BM. Hãy tính a) số đo góc KAN

                                 b) chu vi tam giác MCN 
#Toán lớp 8
1
T
tth_new
7 tháng 8 2019

A A B C D M N #Hình vẽ chỉ mang t/c minh họa K

a) Dễ chứng minh \(\Delta\)DKA = \(\Delta\)BMA.

Suy ra ^KAD = ^MAB. Mà ^MAB + ^MAN + ^NAD = 90o

Nên ^KAD + ^MAN + ^NAD = 90o hay ^KAD + ^NAD = 45o hay ^KAN = 45o

b)Chưa nghĩ ra

Đúng(0)
PT
Pham Trong Bach
28 tháng 2 2019

Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho M A N ^ = 45 0 . Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính : Chu vi tam giác MCN theo a. 
#Toán lớp 8
1
CM
Cao Minh Tâm
28 tháng 2 2019

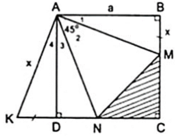
Bài tập tổng hợp chương 1 Hình học 8 | Lý thuyết và Bài tập Toán 8 có đáp án

Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN

Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:

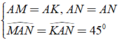Bài tập tổng hợp chương 1 Hình học 8 | Lý thuyết và Bài tập Toán 8 có đáp án ⇒ Δ AMN = Δ AKN ( c - g - c )

⇒ MN = KN (cạnh tương ứng bằng nhau)

Khi đó, chu vi của tam giác MCN là

MC + CN + MN = a - x + a - DN + x + DN = 2a.

Đúng(0)
PT
Pham Trong Bach
4 tháng 4 2018

Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho  M A N ^ = 45 0 . Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính: Chu vi tam giác MCN theo a.
#Toán lớp 8
1
CM
Cao Minh Tâm
4 tháng 4 2018

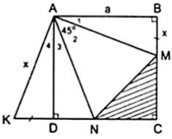
Bài tập: Hình vuông | Lý thuyết và Bài tập Toán 8 có đáp án

Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN

Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:

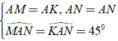Bài tập: Hình vuông | Lý thuyết và Bài tập Toán 8 có đáp án ⇒ Δ AMN = Δ AKN ( c - g - c )

⇒ MN = KN (cạnh tương ứng bằng nhau)

Khi đó, chu vi của tam giác MCN là

MC + CN + MN = a - x + a - DN + x + DN = 2a.

Đúng(0)
H
Huytd
8 tháng 4 2022
Cho hình vuông ABCD nhất định M là 1 điểm lấy trên cạnh BC tia AM cắt DC tại P trên tia đối tia DC lấy điểm N sao cho DN=BM Chứng minh tam giác AND=ABM và tam giác MAN vuông cân Chứng minh tam giác ABM và tam giác PAD đồng dạng và BC^2=BM.DP Qua A vẽ đường thẳng vuông góc với MN tại H và cắt CD tại Q ,MN cắt AD ở I chứng minh AH.AQ=AI.AD và góc...
Đọc tiếp

Cho hình vuông ABCD nhất định M là 1 điểm lấy trên cạnh BC tia AM cắt DC tại P trên tia đối tia DC lấy điểm N sao cho DN=BM 

Chứng minh tam giác AND=ABM và tam giác MAN vuông cân 

Chứng minh tam giác ABM và tam giác PAD đồng dạng và BC^2=BM.DP 

Qua A vẽ đường thẳng vuông góc với MN tại H và cắt CD tại Q ,MN cắt AD ở I chứng minh AH.AQ=AI.AD và góc DAQ=HMQ 
#Toán lớp 8
1
NL
Nguyễn Lê Phước Thịnh
4 tháng 7 2023

a: Xét ΔAND và ΔABM có

góc A chung

AN=DM

AB=AD

=>ΔAND=ΔABM

=>AN=AM

góc NAD=góc BAM

=>góc NAD+góc DAM=góc DAM+góc BAM=90 độ

=>góc NAM=90 độ

=>ΔNAM vuông cân tại A

b: Xét ΔABM và ΔPDA có

góc B=góc D

góc BAM=góc APD

=>ΔABM đồng dạng với ΔPDA

=>AB/BM=PD/AD

=>AB*AD=BM*PD=BC^2
c: Xét ΔAIH và ΔAQD có

góc A chung

góc H=góc D

=>ΔAIH đồng dạng với ΔAQD

=>AI*AD=AH*AQ

Đúng(1)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP