K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 3 2017
3b)
Ta có tg BNK vuông tại K ->BN>BK
Ta có IK=MN(tính chất đoạn chắn)
Ta có : BC+MN=BK+KC+MN=BK+BI+IK=2BK
Vì BK<BN->2BK<2BN->BN>BK/2->BN>BC+MN/2
24 tháng 2 2022
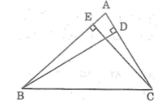
a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
Suy ra: BE=CD
b: Ta có: ΔEBC=ΔDCB
nên \(\widehat{ECB}=\widehat{DBC}\)
hay ΔIBC cân tại I
Ta có: AE+EB=AB
AD+DC=AC
mà AB=AC
và EB=DC
nên AE=AD
Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC
c: Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại I
Do đó: I là trực tâm của ΔABC
Suy ra: AI\(\perp\)BC
mà AK\(\perp\)BC
nên A,I,K thẳng hàng
=>AK,BD,CE đồng quy
CM
7 tháng 6 2017
Trong ΔABD, ta có ∠(ADB) = 90o
Suy ra: BD < AB (đường vuông góc ngắn hơn đường xiên) (1)
Trong ΔAEC, ta có ∠(AEC) = 90o
Suy ra: CE < AC (cạnh huyền lớn hơn cạnh góc vuông) (2)
Cộng từng vế (1) và (2), ta có: BD + CE < AB + AC.
12 tháng 8 2018
Bạn tự vẽ hình nha
1. a) ta có: tg abc cân => AB=AC; AH vừa là trung tuyến vừa là phân giác của tg abc (1)
=> AH là tia phân giác của góc A
b) từ (1) => AH là trung tuyến của tg abc
=> HB=HC
2. ta có: tg abc cân; ab=ac
=> bd và ce vừa là đường cao vừa là trung tuyến của tg abc
=> ad=dc; ab=be ( mà ab=ac)
=> ae=ad
tg abd= tg ace: ab=ac; góc a chung; ae=ad
=> bd=ce
học tốt nha bạn
hình đâu v bạn
Trong tập