Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
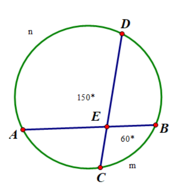
\(\widehat{AMC}\) là có đỉnh ở bên ngoài đường tròn chắn hai cung AC và BD
=>\(\widehat{AMC}=\dfrac{1}{2}\cdot\left(sđ\stackrel\frown{BD}-sđ\stackrel\frown{AC}\right)=\dfrac{1}{2}\left(180^0-60^0\right)=60^0\)
Xét (O) có
ΔBAD nội tiếp
BD là đường kính
Do đó: ΔBAD vuông tại A
=>DA\(\perp\)MB tại A
Xét (O) có
ΔCBD nội tiếp
BD là đường kính
Do đó: ΔCBD vuông tại C
=>BC\(\perp\)MD tại C
Xét tứ giác MAIC có \(\widehat{MAI}+\widehat{MCI}+\widehat{AMC}+\widehat{AIC}=360^0\)
=>\(\widehat{AIC}+60^0+90^0+90^0=360^0\)
=>\(\widehat{AIC}=120^0\)
b: Xét ΔMCB vuông tại C và ΔMAD vuông tại A có
\(\widehat{M}\) chung
Do đó: ΔMCB~ΔMAD
=>\(\dfrac{MC}{MA}=\dfrac{MB}{MD}\)
=>\(MA\cdot MB=MC\cdot MD\)

góc BMC=1/2(sđ cung BC+sđ cung AD)
=>sđ cung AD+70 độ=2*90=180 độ
=>sđ cung AD=110 độ

Đáp án là B
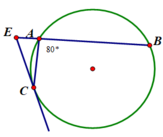
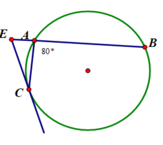
Ta có: ∠(CAB) + ∠(CEA) = 180 0 ⇒ ∠(CEA) = 100 0
Xét tam giác CAE có: ∠(CEA) + ∠(CAE) + ∠(CEB) = 180 0
⇒ ∠(CEB) = 180 0 - 100 0 - 35 0 = 45 0