Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, C/m ∆ AMK = ∆ AMH
Xét∆ AMK và ∆ AMH có:
Góc AMK = góc AMH = 90°
AM chung
Góc MAK = góc MAH (gt)
➡️∆ AMK = ∆ AMH (ch-gn)
b, ✳️ C/m AM vuông góc với QCX
Gọi giao điểm của AM và QC là P.
Xét ∆AQC có: CH vuông góc với AQ
QK vuông góc với AC
mà M là giao điểm của CH và QK
➡️M là trực tâm của ∆ AQC
➡️AP vuông góc với QC (đpcm)
✳️ C/m HK // QC
Xét ∆ AMK = ∆ AMH (cmt)
➡️AK = AH (2 cạnh t/ư)
Nối H với K, gọi giao điểm của AM và HK là D.
Xét ∆ AHK cân tại A (AK = AH)
➡️AD là phân giác đồng thời là đg cao
➡️AD vuông góc với HK
Ta có: AP vuông góc với HK (cmt)
AP vuông góc với QC (cmt)
➡️HK // QC (quan hệ từ vuông góc đến song song)
c, So sánh MC và QC
Xét ∆ MKC có góc K = 90°
➡️Góc KMC là góc nhọn
mà góc QMC là góc kề bù với góc KMC
➡️Góc QMC tù
Xét ∆ QMC có góc QMC tù
➡️QC là cạnh lớn nhất
➡️QC > MC ( quan hệ giữa góc và cạnh đối diện)
còn câu d để mk nghĩ chút đã

a: Xét ΔAMK vuông tại K và ΔAMH vuông tại H có
AM chung
góc MAK=góc MAH
=>ΔAMK=ΔAMH
b: Xét ΔAKQ vuông tại K và ΔAHC vuông tại H có
AK=AH
góc KAQ chung
=>ΔAKQ=ΔAHC
=>AQ=AC
Xét ΔAQC có AH/AQ=AK/AC
nên HK//CQ
Xet ΔCAG có
CH,QK là đường cao
CH cắt QK tại M
=>M là trực tâm
=>AM vuônggóc CQ
c: góc CMQ>90 độ
=>MC<QC

Cm: a) Xét t/giác ABH và t/giác ACH
có AB = AC (gt)
góc AHB = góc AHC = 900 (gt)
AH : chung
=> t/giác ABH = t/giác ACH (ch - cgn)
=> góc BAH = góc HAC (hai góc tương ứng) (Đpcm)
=> BH = CH (hai cạnh tương ứng)
=> H là trung điểm của BC
b) Xét t/giác AMH và t/giác ANH
có góc AMH = góc ANH = 900 (gt)
AH : chung
góc MAH = góc NAH (Cmt)
=> t/giác AMH = t/giác ANH (ch - gn)
=> AM = AN (hai cạnh tương ứng)
=> T/giác AMN là t/giác cân tại A
c) Gọi I là giao điểm của BC và MP
Ta có: T/giác AMH = t/giác ANH (Cmt)
=> MH = HN (hai cạnh tương ứng)
Mà HN = PH (gt)
=> MH = PH
Ta lại có: góc AHM + góc MHB = 900 (phụ nhau)
góc AHN + góc NHC = 900 (phụ nhau)
Và góc AHM = góc AHN (vì t/giác AHM = t/giác AHN)
=> góc MHB = góc NHC
Mà góc NHC = góc BHP
=> góc MHB = góc BHP
Xét t/giác MHI và t/giác PHI
có MH = PH (cmt)
góc MHI = góc IHP (cmt)
HI : chung
=> t/giác MHI = t/giác PHI (c.g.c)
=> MI = PI (hai cạnh tương ứng) => I là trung điểm của MP (1)
=> góc MIH = góc HIP (hai góc tương ứng)
Mà góc MIH + góc HIP = 1800
=> 2.góc MIH = 1800
=> góc MIH = 1800 : 2
=> góc MIH = 900
=> HI \(\perp\)MP (2)
Từ (1) và (2) suy ra HI là đường trung trực của đoạn thẳng MP
hay BC là đường trung trực của đoạc thẳng MP (Đpcm)
d) tự lm
Cm: a) Xét t/giác ABH và t/giác ACH
có AB = AC (gt)
góc AHB = góc AHC = 900 (gt)
AH : chung
=> t/giác ABH = t/giác ACH (ch - cgn)
=> góc BAH = góc HAC (hai góc tương ứng) (Đpcm)
=> BH = CH (hai cạnh tương ứng)
=> H là trung điểm của BC
b) Xét t/giác AMH và t/giác ANH
có góc AMH = góc ANH = 900 (gt)
AH : chung
góc MAH = góc NAH (Cmt)
=> t/giác AMH = t/giác ANH (ch - gn)
=> AM = AN (hai cạnh tương ứng)
=> T/giác AMN là t/giác cân tại A
c) Gọi I là giao điểm của BC và MP
Ta có: T/giác AMH = t/giác ANH (Cmt)
=> MH = HN (hai cạnh tương ứng)
Mà HN = PH (gt)
=> MH = PH
Ta lại có: góc AHM + góc MHB = 900 (phụ nhau)
góc AHN + góc NHC = 900 (phụ nhau)
Và góc AHM = góc AHN (vì t/giác AHM = t/giác AHN)
=> góc MHB = góc NHC
Mà góc NHC = góc BHP
=> góc MHB = góc BHP
Xét t/giác MHI và t/giác PHI
có MH = PH (cmt)
góc MHI = góc IHP (cmt)
HI : chung
=> t/giác MHI = t/giác PHI (c.g.c)
=> MI = PI (hai cạnh tương ứng) => I là trung điểm của MP (1)
=> góc MIH = góc HIP (hai góc tương ứng)
Mà góc MIH + góc HIP = 1800
=> 2.góc MIH = 1800
=> góc MIH = 1800 : 2
=> góc MIH = 900
=> HI ⊥MP (2)
Từ (1) và (2) suy ra HI là đường trung trực của đoạn thẳng MP
hay BC là đường trung trực của đoạc thẳng MP (Đpcm)
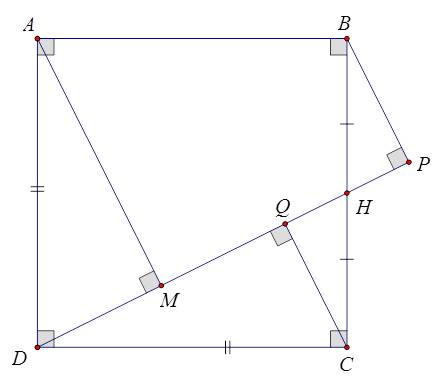
Mình gợi ý nhé
a) Hai tam giác vuông này có hai góc QHC và BHP bằng nhau (đối đỉnh); hai góc HQC và HPB bằng nhau (90o) nên suy ra hai góc QCH và HBP cũng bằng nhau.
Từ đây chứng minh được \(\Delta QHC=\Delta PHB\left(g.c.g\right)\)
b) \(\widehat{DAM}=90^\circ-\widehat{ADM}=\widehat{QDC}=90^\circ-\widehat{QCD}=\widehat{QCH}\)
c) Từ câu b) suy ra \(\Delta DAM=\Delta CDQ\) (g.c.g) nên DM = CQ.