Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, chu vi HCN ABCD là
(15 +24)x2=78 cm
b, Độ dài cạnh DM là
24 :3 =8 cm
độ dài cạnh MC là
8x2=16 cm
diện tích hình tam giác AMC là
16x15 :2=120 cm2
c, diện tích hình thang ABCM là
(24+16)x15:2=300 cm2
tỉ số % diện tích HTG ADM và diện tích HT ABCM là
120:300=0,4=40%
Đ/S .................
BẠN TÍCH CHO MK NHÉ !!!!!!! CÁM ƠN !!!!!!!!
Bạn LINH ĐAN SO CUTE Làm đúng rồi đó .Cảm ơn nha ! AHIHI! 😘😘😘🏆🏆

a, Chu vi hình chữ nhật ABCD là:
\(\left(24+15\right)\times2=78\)(cm2)
b, Độ dài cạnh MC là:
\(24\times\left(1-\frac{1}{3}\right)=16\)(cm)
Diện tích hình tam giác AMC là:
\(16\times15\div2=120\)(cm2)
c, Độ dài cạnh DM là:
\(24-16=8\)(cm)
Diện tích hình tam giác ADM là:
\(8\times15\div2=60\)(cm2)
Diện tích hình thang ABCM là:
\(\left(24+16\right)\times15\div2=300\)(cm2)
Tỉ số phần trăm diện tích của hình tam giác ADM và hình thang ABCM là:
\(60\div300=0,2=20\%\)
Cho hình chữ nhật ABCD có AB = 18 cm, AD = 12 cm, BM = MC, DC = NC. Tính diện tích hình tam giác AMN

Ta có :
S(AMN)=S(ABCD)-{S(ADN)+S(MNC)+S(ABM)} (1)
Diện tích hình chữ nhật là:
S(ABCD)=AB.AD=18.12=216 cm2 (2)
Do DN=NC=> N là trung điểm của DC
Mà ABCD là hình chữ nhật ,nên:
AB=CD, AB=BC
=>DN=NC=CD/2=18/2=9 cm
Do BM=MC=>M là trung điểm của BC
=>BM=MC=BC/2=12/2=6 cm
Diện tích tam giác vuông ADB là:
S(ADN)=1/2.AD.DN=12.9/2=54 cm2 (3)
Diện tích tam giác vuông MNC là:
S(MNC)=1/2.MC.CN=6.9/2=27 cm2 (4)
Diện tích tam giác vuông ABM là:
S(ABM)=1/2.AB.BM=18.6/2=54 cm2 (5)
Thay(2),(3),(4),(5) vào (1) ,ta được:
=>Diện tích tam giác AMN là:
S(AMN)=216-(54+27+54)=81 cm2
Đ s:

Nối AC
cạnh AD = 5+15=20(cm)
MD/AD = 15/20=3/4
Smdc = 3/4 Sadc (MD=3/4AD ,chung chiều cao từ C xuống AD)
Sadc = 1/2 Sabcd(......)
vậy Smdc/Sabcd = (3/4)*(1/2) = 3/8
t...i..c..k mình nha
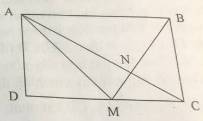
a) MC = 2/5 DC nên DC = 5/2 MC = 5/2 . 10 = 25 cm.
Do đó, AB = CD = 25 cm.
Hình thang ABCM có hai đáy AB, CM và chiều cao BC = AD = 21 cm.
Diện tích hình thang ABCM bằng: (25 + 10) x 21 : 2 = 367,5 (cm2)
b) Hạ AH \(\perp\) BM, CK \(\perp\) BM.
Ta có \(\dfrac{S_{ABM}}{S_{BCM}}=\dfrac{AB}{MC}=\dfrac{5}{2}\) (vì cùng chiều cao, tỉ lệ diện tích bằng tỉ lệ hai đáy), do đó \(\dfrac{AH}{CK}=\dfrac{S_{ABM}}{S_{BCM}}=\dfrac{5}{2}\) (chung đáy, tỉ lệ diện tích bằng tỉ lệ hai chiều cao)
\(\dfrac{S_{AMN}}{S_{CMN}}=\dfrac{AH}{CK}=\dfrac{5}{2}\Rightarrow\dfrac{S_{CMN}}{S_{AMC}}=\dfrac{2}{7}\)
\(S_{AMC}=\dfrac{1}{2}\times AD\times MC=\dfrac{1}{2}\times21\times10=105\left(cm^2\right)\)
\(S_{CMN}=\dfrac{2}{7}\times105=30\left(cm^2\right)\)