Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
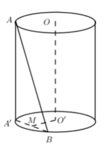
Phương pháp :
+) Xác định mặt phẳng (P) chứa AB và song song với OO’.
+) d(OO’;AB) = D(OO’;(P))
Cách giải :
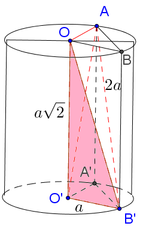
Dựng AA’//OO’ ta có: (OO’;AB) = (AA’;AB) = A’AB = 300
Gọi M là trung điểm của A’B ta có:
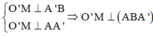
![]()
![]()
=>d(OO’;AB) = d(OO’;(ABA’)) = d(O’;(ABA’)) = O’M
Xét tam giác vuông ABA’ có ![]()
Xét tam giác vuông O’MB có 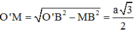

Chọn đáp án C.
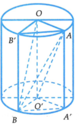
Kẻ các đường sinh AA', BB' của hình trụ (T).
Khi đó
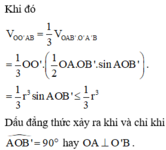
Như vậy, khối tứ diện có thể tích lớn nhất bằng
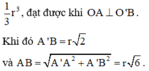

Phương pháp:
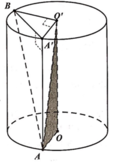
+ Gọi C là hình chiếu của A lên mặt đáy chứa đường tròn O ' ; R và D là hình chiếu của B lên mặt đáy chứa đường tròn (O;R).
+) Tính thể tích lăng trụ đứng O A D . O ' C B , từ đó suy ra thể tích tứ diện OO'AB và đánh giá.
Cách giải:
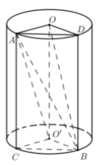

Chọn: D

Đáp án B
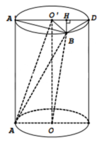
Kẻ đường sinh AA’, gọi D là điểm đối xứng A’ qua tâm O’.
Kẻ BH vuông góc với A ' D ⇒ B H ⊥ A O O ' A ' ⇒ V O O ' A B = 1 3 . B H . S Δ O O ' A
Mà S Δ O O ' A = 1 2 . O O ' . O A = 2 a 2 ⇒ V O O ' A B = 2 a 2 3 x B H
Để V O O ' A B lớn nhất ⇔ B H = B O ' H ≡ O ' ⇒ A ' B = 2 a 2
Tam giác AA’B vuông tại A’, có tan A B A ' ^ = A A ' A ' B = 2 a 2 a 2 = 1 2
Vậy A B ; O ' ^ = A B ; A ' B ^ = A B A ' ^ = α ⇒ tan α = 1 2



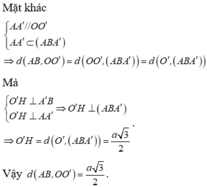

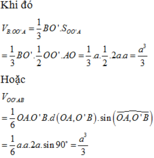
Chọn đáp án D
Cách 1: Kẻ đường sinh AF và BE như hình vẽ.
Cách 2: Sử dụng công thức tính nhanh