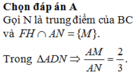Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

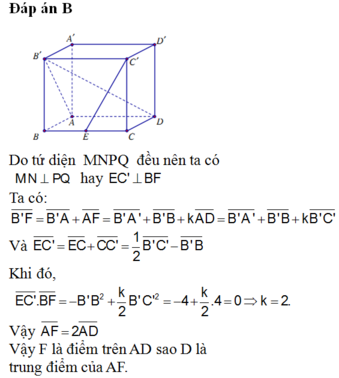
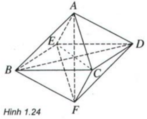
Giả sử bát diện đều ABCDEF có cạnh bằng a.
B, C, D, E cách đều A và F suy ra B, C, D, E cùng nằm trên mặt phẳng trung trực của đoạn thẳng AF
Trong mp (BCDE), ta có BC = CD = DE = EB (= a)
⇒ BCDE là hình thoi
⇒ BD ⊥ EC và BD, EC cắt nhau tại trung điểm mỗi đường.
Chứng minh tương tự ta suy ra AF và BD, AF và CE vuông góc nhau và cắt nhau tại trung điểm mỗi đường.

Đáp án C
![]()
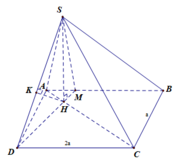
![]()
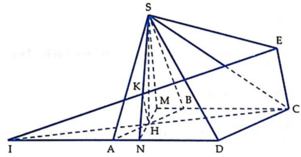
⇒ A C ⊥ D M
Vì S H ⊥ ( A B C D ) ⇒ D H ⊥ ( S A C )
từ H kẻ H K ⊥ S D
⇒ H K là khoảng cách cần tính.
Ta có D H H M = D C A M = 4 ⇔ D H D M = 4 5
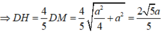
Áp dụng hệ thức lượng trong tam giác vuông.
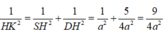
⇒ H K = 2 a 3