Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

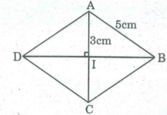
Áp dụng Pi-ta-go vào tam giác vuông IAB, ta có: A B 2 = A I 2 + I B 2
⇒ I B 2 = A B 2 - A I 2 = 25 – 9 = 16
⇒ IB = 4(cm).
AC = 2AI = 2.3 = 6 (cm)
BD = 2IB = 2.4 = 8 (cm)
S A B C D = 1/2 AC.BD = 1/2 .6.8 = 24 ( c m 2 )

Do ABCD là hình thoi nên hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
Diện tích tam giác ABC là
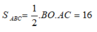
Suy ra: BO.AC = 32
Diện tích hình thoi ABCD là:
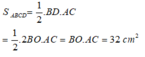
Chọn đáp án B

VÌ ABCD là hình thoi nên O là trung điểm của AC và BD
Suy ra: AC = 2OA = 2.3 = 6cm
Và BD = 2.OB = 2.5= 10cm
Diện tích hình thoi là:
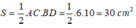
Chọn đáp án A

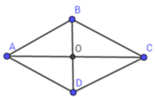
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 20 2 − 16 2 = 12
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.12.16 = 384 (cm2)
Đáp án cần chọn là: A

Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 10 2 − 6 2 = 8
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.8.6 = 96 (cm2)
Đáp án cần chọn là: B

Xét tam giác ABD:
E là trung điểm AB (gt).
H là trung điểm AD (gt).
\(\Rightarrow\) EH là đường trung bình.
\(\Rightarrow\) EH // BD; EH = \(\dfrac{1}{2}\) BD (Tính chất đường trung bình). (1)
Xét tam giác CBD:
F là trung điểm BC (gt).
G là trung điểm CD (gt).
\(\Rightarrow\) FG là đường trung bình.
\(\Rightarrow\) FG // BD; FG = \(\dfrac{1}{2}\) BD (Tính chất đường trung bình). (2)
Xét tamgiacs ACD:
H là trung điểm AD (gt).
G là trung điểm CD (gt).
\(\Rightarrow\) HG là đường trung bình.
\(\Rightarrow\) HG // AC (Tính chất đường trung bình).
Mà AC \(\perp\) BD (Tứ giác ABCD là hình thoi).
\(\Rightarrow\) HG \(\perp\) BD.
Lại có: EH // BD (cmt).
\(\Rightarrow\) EH \(\perp\) HG.
Từ (1) và (2) \(\Rightarrow\) EH // FG; EH = FG.
\(\Rightarrow\) Tứ giác EFGH là hình bình hành (dhnb).
Mà EH \(\perp\) HG (cmt).
\(\Rightarrow\) Tứ giác EFGH là hình chữ nhật (dhnb).
b) Tứ giác ABCD là hình thoi (gt).
\(\Rightarrow\) AC cắt BD tại trung điểm mỗi đường (Tính chất hình thoi).
Mà I là giao điểm của AC và BD (gt.)
\(\Rightarrow\) I là trung điểm của AC và BD.
\(\Rightarrow\left\{{}\begin{matrix}AI=\dfrac{1}{2}AC=\dfrac{1}{2}.8=4\left(cm\right).\\IB=\dfrac{1}{2}BD=\dfrac{1}{2}.10=5\left(cm\right).\end{matrix}\right.\)
Xét tam giác ABI: AI \(\perp\) BI (AC \(\perp\) BD).
\(\Rightarrow\) Tam giác ABI vuông tại I.
\(\Rightarrow S_{\Delta ABI}=\dfrac{1}{2}AI.IB=\dfrac{1}{2}.4.5=10\left(cm^2\right).\)
\(\perp\)

Áp dụng Pi-ta-go vào tam giác vuông IAB, ta có: \(AB^2=AI^2+IB^2\)
\(\Rightarrow IB^2=AB^2-AI^2=25-9=16cm\)
\(\Rightarrow IB=4\left(cm\right)\)
\(AC=2AI=2.3=6\left(cm\right)\)
\(BD=2IB=2.4=8\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.6.8=24\left(cm^2\right)\)
Chúc bạn học tốt !!!