Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để so sánh diện tích hai tam giác AMC và BMN, ta cần biết thêm thông tin về các độ dài cạnh của hình thang ABCD và vị trí của các điểm A, B, C, D, M, N trên hình thang. Trong đề bài không cung cấp đủ thông tin này, nên không thể trả lời câu hỏi này.
b) Để tính diện tích hình thang ABCD, ta cần biết độ dài hai đáy AB và CD, và chiều cao của hình thang. Tuy nhiên, trong đề bài không cung cấp đủ thông tin này, nên không thể tính được diện tích hình thang ABCD.

Xét \(\Delta\) ACN và tg BCN có chung cạnh CN và đường cao từ A\(\rightarrow\)CD = đường cao từ B xuống CD nên:
\(S_{ACN}=S_{BCN}\Rightarrow S_{AMC}+S_{CMN}=S_{BMN}+S_{CMN}\)
\(\Rightarrow S_{AMC}=S_{CMN}\)
b) Xét \(\Delta\) CMN và tg BMN có chung đường cao từ N \(\rightarrow\) BC nên:
\(\dfrac{S_{CMN}}{S_{BMN}}=\dfrac{MC}{MB}=\dfrac{1}{2}\Rightarrow S_{BMN}=2\times S_{CMN}\)
Mà \(S_{BMN}=S_{AMC}\Rightarrow S_{AMC}=2\times S_{CMN}\)
Xét \(\Delta\) AMC và tg AMB có chung đường cao từ A\(\rightarrow\)BC nên:
\(\dfrac{S_{AMC}}{S_{AMB}}==\dfrac{MC}{MB}=\dfrac{1}{2}\Rightarrow S_{AMB}=2\times S_{AMC}=2\times2\times S_{CMN}=4\times S_{CMN}\)
\(\Rightarrow S_{ABC}=S_{AMB}+S_{AMC}=4\times S_{CMN}+2\times S_{CMN}=6\times S_{CMN}\)
Xét \(\Delta\)ABC và tg ACD có đường cao từ C\(\rightarrow\)AB = đường cao từ A\(\rightarrow\)CD nên:
\(\dfrac{S_{ABC}}{S_{ADC}}=\dfrac{AB}{CD}=\dfrac{1}{2}\Rightarrow S_{ACD}=2\times S_{ABC}=2\times6\times S_{CMN}=12\times S_{CMN}\)
\(\Rightarrow S_{ABCD}=S_{ABC}+S_{ACD}=6\times S_{CMN}=12\times S_{CMN}\)
\(=18\times S_{CMN}=18\times112,5=2025\left(cm^2\right)\)

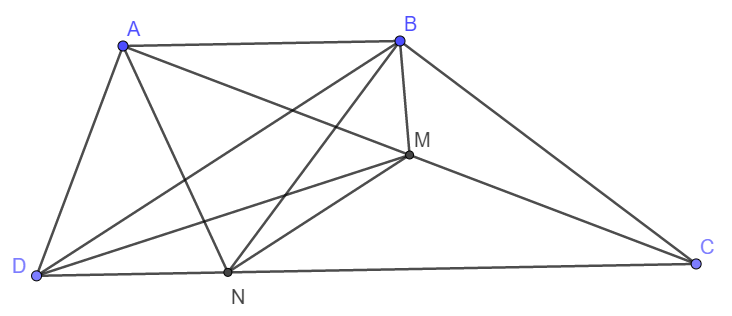
a) Ta thấy hai tam giác MN và DMN có chung cạnh MN.
Lại có do DB // MN nên chiều cao hà từ B và D xuống MN là bằng nhau.
Vậy diện tích tam giác BNM bằng diện tích tam giác DMN.
b) Ta thấy \(AM=MC\Rightarrow\frac{S_{ABM}}{S_{BAC}}=\frac{1}{2};\frac{S_{ADM}}{S_{DAC}}=\frac{1}{2}\)
Vậy nên \(\frac{S_{ABM}+S_{ADM}}{S_{BAC}+S_{DAC}}=\frac{1}{2}\Rightarrow\frac{S_{ABMD}}{S_{ABCD}}=\frac{1}{2}\)
\(\Rightarrow S_{ABMD}=16:2=8\left(cm^2\right)\)
Lại có \(S_{ABMD}=S_{ABMND}-S_{DMN}=S_{ABND}+S_{BMN}-S_{DMN}\)
\(=S_{ABND}\) hay \(S_{ABND}=8cm^2\)

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Lê Hoàng - Toán lớp 5 - Học toán với OnlineMath
co ai biet lam ko lam on lam nhanh len cho minh voi minh cho