Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~

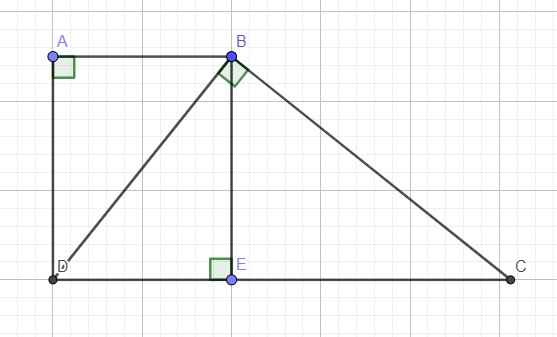
Kẻ BE vuông góc CD \(\Rightarrow ABED\) là hcn (tứ giác 4 góc vuông) \(\Rightarrow AB=DE\)
Đặt \(AB=x>0\)
Áp dụng định lý Pitago cho tam giác vuông ABD:
\(AB^2+AD^2=BD^2\Leftrightarrow BD^2=x^2+144\) (1)
Áp dụng hệ thức lượng cho tam giác vuông BDC:
\(BD^2=DE.DC\Leftrightarrow BD^2=25x\) (2)
(1);(2) \(\Rightarrow x^2+144=25x\Rightarrow x^2-25x+144=0\Rightarrow\left[{}\begin{matrix}x=16\\x=9\end{matrix}\right.\)
- Với \(AB=16\left(cm\right)\Rightarrow BD=\sqrt{AD^2+AB^2}=20\left(cm\right)\)
\(BC=\sqrt{DC^2-BD^2}=15\left(cm\right)\)
- Với \(AB=9\left(cm\right)\Rightarrow BD=\sqrt{AD^2+AB^2}=15\left(cm\right)\)
\(BC=\sqrt{DC^2-BD^2}=20\left(cm\right)\)

Tham Khảo tại link
https://hoc24.vn/cau-hoi/cho-abcd-la-hinh-thang-vuong-tai-a-va-d-duong-cheo-bd-vuong-goc-voi-bc-biet-ad-12-cm-dc-25-cm-tinh-do-dai-ab-bc-bd.189488030358
Hạ BE ⊥ CD ( E ∈ CD )
Xét △BCD vuông tại B có BE ⊥ CD. Áp dụng hệ thức lượng trong tam giác vuông, ta có:
BE\(^2\) = DE . EC hay DE . ED = 12\(^2\) =144 cm (*)
Ta có:
DE + EC = CD = 25 cm ⇒ DE = 25 − EC
Thay vào (*) ta có: ( 25 − EC ) . EC = 144
⇒ 25 EC − EC\(^2\) = 144
⇒ EC\(^2\) − 25 EC + 144 = 0
⇒ ( EC − 9 )( EC − 16 ) = 0
\(\Rightarrow\left[{}\begin{matrix}EC=9\\EC=16\end{matrix}\right.\)
Nếu EC = 9 cm ⇒ DE = 16 cm
Xét tứ giác ABED có ˆ\(\widehat{A}=\widehat{D}=\widehat{E}=90^0\) nên là hình chữ nhật
⇒ AB = DE ; AD = BE
Hay AB = 16 cm và BE = 12cm
Áp dụng định lý Pytago trong tam giác vuông BED ta có: \(BD^2=BE^2+DE^2=12^2+16^2=400\) ⇒ BD = 20 cm
Áp dụng định lý Pytago trong tam giác vuông BEC, ta có: \(BC^2=BE^2+CE^2=12^2=92=225\)
⇒ BC = 15 cm
Tương tự với trường hợp EC = 16cm ⇒ DE = 9 cm
Ta suy ra: AB = 9 cm ; BD = 15 cm và BC = 20 cm

bạn bấm vào chữ'' đúng 0'' sẽ hiện ra đáp án