Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ADHB có
\(\widehat{DAB}=\widehat{ADH}=\widehat{BHD}=90^0\)
Do đó: ADHB là hình chữ nhật
mà AB=AD
nên ADHB là hình vuông

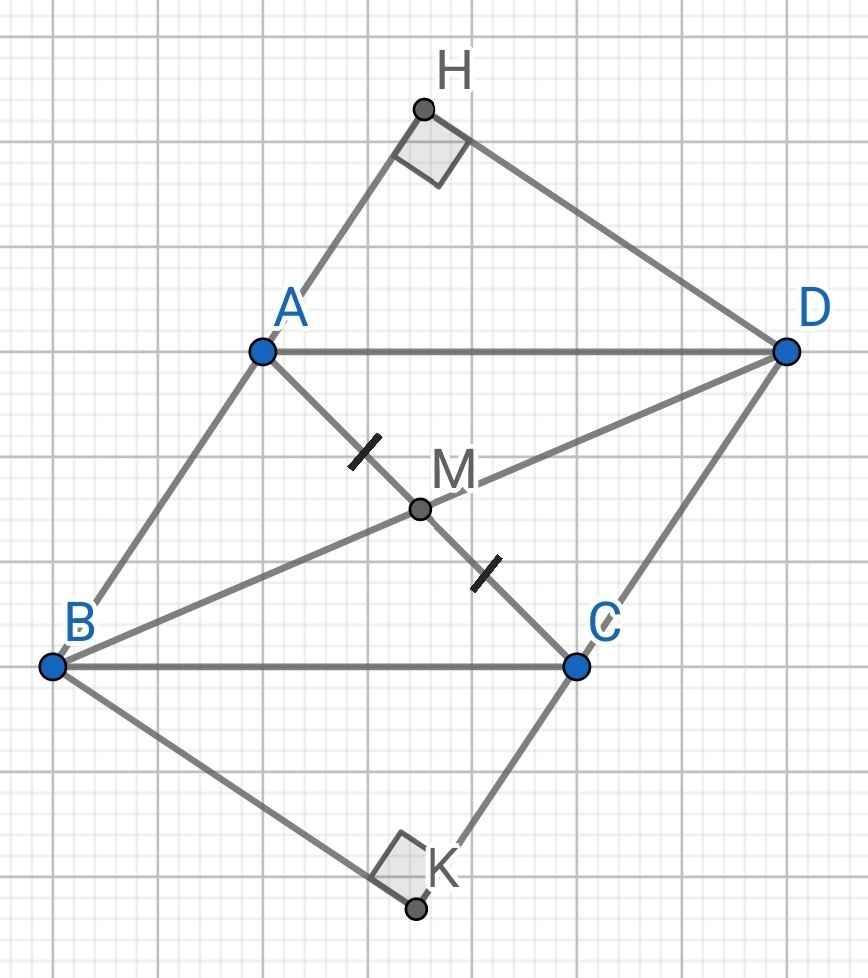 a) Do BM là đường trung tuyến của ∆ABC (gt)
a) Do BM là đường trung tuyến của ∆ABC (gt)
⇒ M là trung điểm của AC
Do D và B đối xứng qua M (gt)
⇒ M là trung điểm của BD
Tứ giác ABCD có:
M là trung điểm của AC (cmt)
M là trung điểm của BD (cmt)
⇒ ABCD là hình bình hành
b) Do ABCD là hình bình hành (cmt)
⇒ AB // CD
Mà DH ⊥ AB
⇒ DH ⊥ AC
c) Do ABCD là hình bình hành
⇒ AB // CD
Mà BK ⊥ CD
⇒ BK ⊥ AB
⇒ ∠KBH = 90⁰
Tứ giác BHDK có:
∠BKD = ∠KBH = ∠BHD = 90⁰
⇒ BHDK là hình chữ nhật
Mà M là trung điểm BD
⇒ M là trung điểm của HK
⇒ M, H, K thẳng hàng
Do đó chứng minh MH ⊥ MK là sai. Em xem lại đề ở câu c nhé

Gọi K là trung điểm của HD
Xét ΔHDC có
K,M lần lượt là trung điểm của HD,HC
=>KM là đường trung bình của ΔHDC
=>KM//DC và \(KM=\dfrac{DC}{2}\)
KM//DC
AB//DC
Do đó: KM//AB
KM//DC
DC\(\perp\)AD
Do đó: \(MK\perp AD\)
Xét ΔADM có
MK,DHlà đường cao
MK cắt DH tại K
Do đó: K là trực tâm của ΔADM
=>AK\(\perp\)DM
mà BM\(\perp\)DM
nên AK//BM
Xét tứ giác ABMK có
AB//MK
AK//BM
Do đó: ABMK là hình bình hành
=>MK=AB
=>CD=2AB

a: Xét tứ giác ABHD có
\(\widehat{BAD}=\widehat{ADH}=\widehat{BHD}=90^0\)
=>ABHD là hình chữ nhật
Hình chữ nhật ABHD có AB=AD
nên ABHD là hình vuông
=>AB=BH=HD=DA
mà \(AB=AD=\dfrac{DC}{2}\)
nên \(BH=DH=\dfrac{DC}{2}\)
DH=DC/2
=>H là trung điểm của DC
Xét ΔDBC có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔDBC cân tại B(2)
Xét ΔBDC có
BH là đường trung tuyến
\(BH=\dfrac{DC}{2}\)
Do đó: ΔBDC vuông tại B(1)
Từ (1) và (2) suy ra ΔBDC vuông cân tại B
b: AB=HD
HD=HC
Do đó: AB=HC
Xét tứ giác ABCH có
AB//CH
AB=CH
Do đó: ABCH là hình bình hành
=>AC cắt BH tại trung điểm của mỗi đường
mà M là trung điểm của BH
nên M là trung điểm của AC
c: \(\widehat{ADI}+\widehat{IAD}=90^0\)(ΔADI vuông tại I)
\(\widehat{ACD}+\widehat{IAD}=90^0\)(ΔADC vuông tại D)
Do đó: \(\widehat{ADI}=\widehat{ACD}\)
mà \(\widehat{ACD}=\widehat{BAC}\)(hai góc so le trong, AB//CD)
nên \(\widehat{BAC}=\widehat{ADI}\)

Sửa đề: DH vuông góc AC
1: Xét ΔHDC có
M,N lần lượt là trung điểm của HD,HC
nên MN là đường trung bình
=>MN//DC và MN=DC/2
=>MN//AB và MN=AB
=>ABNM là hình bình hành
2: NM//AB
=>NM vuông góc AD
Xét ΔAND có
DH,NM là các đường cao
DH cắt NM tại M
=>M là trực tâm
3: Xét ΔHDC có
E,N lần lượt là trung điểm của CD,CH
nên EN là đường trung bình
=>EN//HD và EN=HD/2
=>EN//HM và EN=HM
=>HMEN là hình bình hành
=>MN đi qua trung điểm của HE
Gọi K là trung điểm của HD
Xét ΔHDC có
K,M lần lượt là trung điểm của HD,HC
=>KM là đường trung bình
=>KM//DC và KM=DC/2
=>KM//AB và KM=AB
=>ABMK là hình bình hành
=>AK//BM
MK//DC
DC vuông góc AD
=>MK vuông góc AD
Xét ΔADM có
MK,DH là đường cao
MK cắt DH tại K
Do đó: K là trực tâm
=>AK vuông góc DM
mà BM//AK
nên BM vuông góc DM
Cảm ơn anh.