Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M
Nối A với C
Hai tam giác ABC và ADC có chiều cao hạ xuống từ đỉnh C và đỉnh A bằng nhau ( đều là chiều cao của hình thang ) mà đáy \(AB=\frac{1}{3}\)đáy \(CD\)
\(\Rightarrow S_{ABC}=\frac{1}{3}S_{ADC}\)
Vì hai tam giác AMB và AMC có chung đáy AM; chiều cao của tam giác AMB là AB còn chiều cao của tam giác AMC là CD mà \(AB=\frac{1}{3}CD\)
\(\Rightarrow S_{AMB}=\frac{1}{3}S_{AMC}\)
Do \(\frac{S_{ABC}}{S_{ADC}}=\frac{1}{3}\Rightarrow\frac{S_{ABC}}{S_{ABC}+S_{ADC}}=\frac{1}{1+3}\Leftrightarrow\frac{S_{ABC}}{S_{ABCD}}=\frac{1}{4}\)
\(\Rightarrow S_{ABC}=\frac{1}{4}.16=4\left(cm^2\right)\)
Mà \(\frac{S_{ABM}}{S_{ACM}}=\frac{1}{3}\Rightarrow\frac{S_{ABM}}{S_{ACM}-S_{ABM}}=\frac{1}{3-1}\Leftrightarrow\frac{S_{ABM}}{S_{ABC}}=\frac{1}{2}\)
\(\Rightarrow S_{ABM}=\frac{1}{2}.4=2\left(cm^2\right)\)
Vậy diện tích hình tam giác MAB là \(2cm^2.\)
( Bạn vẽ hình ra )
( Vẽ thêm hình nữa và hạ từ đỉnh B xuống đáy DC sao cho trong hình thang cuông có đủ 4 hình tam giác )
Ta có DT của cả 4 hình tam giác trng hình thang vuông ABCD đều bằng nhau vì tất cả đều có chung đáy AB và chiều cao AD .
DT hình tam giác ABD là :
16 : 4 = 4 ( cm2 )
DT BDM = 1/3 DT CDM
DT tam giác BDC là :
16 - 4 = 12 ( cm2 )
DT BDM = 1/2 DT BDC
DT tam giác BDM là :
12 : 2 = 6 ( cm2 )
DT tam giác MAB là :
6 - 4 = 2 ( cm2 )
Đáp số : 2 cm2 .

Xét tam giác ABC và ACD có cùng chiều cao chính là chiều cao hình thang, đáy dc gấp 3 đáy AB => S_ACD gấp 3 lần S_ABC.
Vậy diện tích tam giác ABC là : 16 : (3 + 1) = 4 (cm2)
Xét tam giác MAB và MAC có chung đáy MA mà CD gấp 3 lần AB (vì AB và CD cùng vuông góc với MD) => S_MAB = 1/3 S_MAC => S_MAB = 1/2 S_ABC
Vậy diện tích MAB là : 4 : (3-1) = 2 (cm2)

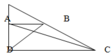
Nối B với D và nối A với C.
Xét 2 tam giác: BAD và CAD. Có:
-Chung đáy AD
-Chiều cao AB = 1 3 CD
=> S.BAD = 1 3 S.CAD
Do đó: S.BAD = 1 4 S.ABCD
S.BAD = 16 : 4 = 4 ( c m 2 )
S.BDC = 16 - 4 = 12 ( c m 2 )
Tam giác BDM và tam giác CDM có chung đáy MD và chiều cao BA = 1 3 CD
Do đó: S.BDM = 1 3 S.CDM
Suy ra S.BDM = 1 2 S.BDC
Mà S.BDC = 12 c m 2 . Nên S.BDM = 12 : 2 = 6 ( c m 2 )
Vì S.MAB = S.BDM - S.BAD . Nên S.MAB = 6 – 4 = 2 ( c m 2 )
Đáp số: S.MAB = 2 ( c m 2 )

S(ABD) = 1/3 S(ACD)
Mà hai hình này chung đáy AD => chiều cao hạ từ B = 1/3 chiều cao hạ từ C.
=> S(MAB) = 1/3 S(MAC)
=> S(MAB) = 1/2 S(ABC)
S(ABC) = 1/3 S(ACD) = 1/4 S(ABCD)
=> S(MAB) = 1/2 x 1/4 = 1/8 S(ABCD)
Vậy S(MAB) = 16 x 1/8 = 2 cm2
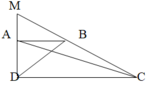

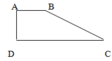
Đầu tiên ta nối B với D
Ta có : \(\Delta ABD=\frac{1}{3}\Delta BDC\)vì hai tam giác có chung cao AD nhưng đáy AB = 1/3 đáy CD
\(\Delta MDB=\frac{1}{3}\Delta MDC\)vì hai tam giác có chung đáy MD và cao AB = 1/3 cao CD
Vậy \(\Delta MDC=\Delta BDC+\Delta MBD\)
\(\Delta MDC=\Delta BDC+\frac{1}{3}\Delta MDC\Leftrightarrow\Delta BDC=\frac{2}{3}\Delta MDC\)
\(\Leftrightarrow\Delta MBD=\frac{1}{2}\Delta BDC\)vì tam giác MBD = 1/3 tam giác MDC nhưng tam giác BDC = 1/3 x 2 = 2/3 tam giác MDC\
\(\Rightarrow\Delta MBD=\frac{1}{2}\Delta BDC=\frac{3}{4}\cdot\frac{1}{2}ABCD=16\cdot\frac{3}{4}\cdot\frac{1}{2}=12\cdot\frac{1}{2}=6\left(cm^2\right)\)
\(ABCD=\Delta BDC+\Delta ABD=12+4\)
Thế vào ta có :
\(\Delta MBD=\Delta ABD+\Delta MAB=4+\Delta MAB\Leftrightarrow6=4+\Delta MAB\)
\(\Rightarrow\Delta MAB=2\left(cm^2\right)\)